
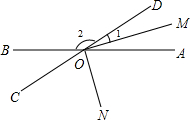
 已知,如图,直线AB,CD相交于点O,OM平分∠AOD,且∠1:∠2=1:4,ON平分∠AOC,求∠BON的度数.
已知,如图,直线AB,CD相交于点O,OM平分∠AOD,且∠1:∠2=1:4,ON平分∠AOC,求∠BON的度数. 分析 设∠1=x°,则∠2=(4x)°,根据角平分线得到∠AOD=2∠1=(2x)°,利用平角求出x,求出∠AOC的度数,即可解答.
解答 解:设∠1=x°,则∠2=(4x)°,
∵OM平分∠AOD,
∴∠AOD=2∠1=(2x)°,
∵∠2+∠AOD=180°,
∴4x+2x=180,
解得:x=30,
∴∠AOD=60°,
∴∠AOC=180°-∠AOD=180°-60°=120°,
∵ON平分∠AOC,
∴∠CON=$\frac{1}{2}$∠AOC=60°,
∵∠BOC=∠AOD=60°,
∴∠BON=∠BOC+∠CON=60°+60°=120°.
点评 本题考查了对顶角,邻补角,解决本题的关键是设∠1=x°,利用平角求出x,求出∠AOC的度数,即可解答.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.
甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图1所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 85 | 1 |
| 乙 | 80 | 1060 | 80 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com