
【题目】如图所示,一块等腰直角三角形铁板,通过切割焊接成一个含有45°角的平行四边形,设计一种简要的方案并给出正确的理由. 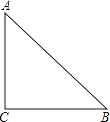
【答案】解:如图,取AC、BC的中点E、D,连接ED,沿ED切割,固定点E,△ECD旋转180°使C点与A点重合即可. 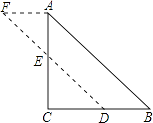
理由:在Rt△ABC中,
∵AC=BC,∠B=45°,
又∵E、D分别是AC、BC的中点,
∴EC=DC
∴∠CED=∠CDE=45°
∴∠AEF=∠CED=45°
∴∠AEF+∠AED=∠CED+∠AED=180°
∴F、E、D在一条直线上.
又∵∠EAF=∠C=90°
∴AF∥CD.
又∵AF=CD=DB,
∴四边形AFDB是平行四边形,且∠B=45°
【解析】∵这是一块等腰直角三角形铁板,已经包含45°的角.∴应用到题中45°的角,利用全等进行割补,应遵循简单易行的原则.
【考点精析】掌握等腰直角三角形和平行四边形的判定与性质是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


科目:初中数学 来源: 题型:
【题目】某人购进一批苹果,到市场零售,已知销售额y(元)与卖出的苹果数量x(千克)的关系如表所示:则y与x之间的关系式为__________
数量x(千克) | 2 | 3 | 4 | 5 | … |
销售额y(元) | 7.2 | 10.8 | 14.4 | 18.0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连结BE、CF.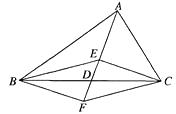
(1)图中的四边形BFCE是平行四边形吗?为什么?
(2)若AB=AC,其它条件不变,那么四边形BFCE是菱形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我市2017年中考数学学科各分数段成绩分布情况,从中抽取180名考生的中考数学成绩进行统计分析.在这个问题中,样本是指( )
A. 180 B. 被抽取的180名考生
C. 被抽取的180名考生的中考数学成绩 D. 我市2017年中考数学成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
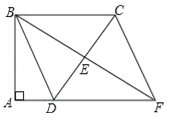
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据. 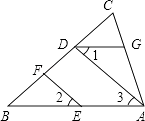
【解】∵EF∥AD(已知)
∴∠2=()
又∵∠1=∠2(已知)
∴∠1=∠3(等式性质或等量代换)
∴AB∥()
∴∠BAC+=180°()
又∵∠BAC=70°(已知)
∴∠AGD=110°(等式性质)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com