
分析 由于k的符号不确定,因此一次函数的增减性不确定,故需分情况讨论,只需分k>0或k<0两种情况讨论,然后利用一次函数的增减性,就可解决问题.
解答 解:①当k>0时,
由题可得:当x=-1时y=3,当x=2时y=5,
∴$\left\{\begin{array}{l}{-k+b=3}\\{2k+b=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=\frac{11}{3}}\end{array}\right.$,
∴该函数的解析式为y=$\frac{2}{3}$x+$\frac{11}{3}$;
②当k<0时,
由题可得:当x=-1时y=5,当x=2时y=3,
∴$\left\{\begin{array}{l}{-k+b=5}\\{2k+b=3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=\frac{13}{3}}\end{array}\right.$
∴该函数的解析式为y=-$\frac{2}{3}$x+$\frac{13}{3}$.
综上所述:该函数的解析式为y=$\frac{2}{3}$x+$\frac{11}{3}$或y=-$\frac{2}{3}$x+$\frac{13}{3}$.
点评 本题主要考查了运用待定系数法求一次函数的解析式、一次函数的增减性、解二元一次方程组等知识,在解决问题的过程中运用了分类讨论及待定系数法等重要的数学思想方法,应熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,A(t,0),B(t+$\sqrt{3}$,0),对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.
在平面直角坐标系xOy中,A(t,0),B(t+$\sqrt{3}$,0),对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
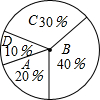 某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机调查了部分学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.并结合调查数据作出如图所示的扇形统计图,根据统计图提供的信息,可估算出该校植树量达到6棵的学生有( )
某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机调查了部分学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.并结合调查数据作出如图所示的扇形统计图,根据统计图提供的信息,可估算出该校植树量达到6棵的学生有( )| A. | 26名 | B. | 52名 | C. | 78名 | D. | 104名 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com