
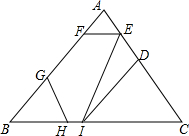
 如图,D,E,F,G,H,I是三角形ABC三边上的点,连结EI,EF∥BC,GH∥AC,DI∥AB.
如图,D,E,F,G,H,I是三角形ABC三边上的点,连结EI,EF∥BC,GH∥AC,DI∥AB.分析 (1)根据同旁内角的定义解答即可;
(2)根据平行线的性质得到∠FEC+∠C=180°,∠GHC+∠C=180°,根据余角的性质即可得到结论;
(3)根据平行线的性质得到∠FEC+∠C=180°,求得∠FEC=180°-∠C=124°,根据角平分线的定义得到∠FEI=$\frac{1}{2}$∠FEC=62°,由平行线的性质得到∠DIC=∠B=50°,即可得到结论.
解答 解:(1)与∠IEC是同旁内角的角是:∠C、∠EDI、∠EIC、∠EID;
(2)∠GHC=∠FEC,
理由:∵EF∥BC,
∴∠FEC+∠C=180°,
∵GH∥AC,
∴∠GHC+∠C=180°,
∴∠GHC=∠FEC;
(3)∵EF∥BC,∠C=56°,
∴∠FEC+∠C=180°,
∴∠FEC=180°-∠C=124°,
∵EI平分∠FEC,
∴∠FEI=$\frac{1}{2}$∠FEC=62°,
∴∠FEI=∠EIC=62°,
∵DI∥AB,∠B=50°,
∴∠DIC=∠B=50°,
∴∠EID=∠EIC-∠DIC=12°.
点评 本题考查了平行线的性质,角平分线的定义,同旁内角的定义,熟练掌握平行线的性质是解题的关键.


科目:初中数学 来源:2016-2017学年新疆乌鲁木齐市八年级下学期第一次月考数学试卷(解析版) 题型:单选题
在△ABC中,∠C=90°,AC=4,BC=2,则下面正确的是( )
A. 高CD为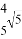 B. 斜边AB为
B. 斜边AB为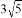
C. △ABC的面积为8 D. 周长为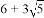
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④⑤⑧ | B. | ②③⑤⑥⑦⑧ | C. | ①③④⑤⑥⑧ | D. | ①②④⑤⑦⑧ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com