Question

如图所示，堆放的一堆钢管共110根，最上面的一层有5根，每往下一层就增加一根，如果每根钢管的直径为10厘米，那么这堆钢管的总高度是________厘米．

Answer 1

（10+）
分析：设110根钢管共放x层，根据最上面的一层有5根，每往下一层就增加一根，总结规律表示出最底层的根数，利用最上面的5根加上表示出的最底层的根数，乘以项数x，再除以2表示出钢管的总数，等于110列出关于x的方程，求出方程的解得到x的值，然后根据题意画出相应的图形，可得出这堆钢管的总高度等于等边三角形ABC的高与一根钢管的直径相加，根据等边三角形ABC的边长为10个钢管的直径，由每根钢管的直径求出等边三角形的边长，过A作AD垂直于BC，根据三线合一得到D为BC中点，求出BD的长，根据勾股定理求出AD的长，用求出的AD长加上一根钢管的直径，即为这堆钢管的总高度．
解答：设这堆钢管110根一共放x层，则最底层有[5+（x-1）]=（x+4）根，
根据题意得：=110，即（x-11）（x+20）=0，
解得：x=11或x=-20（舍去），
∴堆放的一堆钢管共放11层，
根据题意画出相应的图形，如图所示：

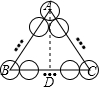
∵每根钢管的直径为10厘米，
∴△ABC为边长为100厘米的等边三角形，
过A作AD⊥BC，则有D为BC的中点，
在直角三角形ABD中，AB=100厘米，BD=50厘米，
根据勾股定理得：AD==50（厘米），
则这堆钢管的总高度是（10+50）厘米．
故答案为：（10+50）
点评：此题考查了两圆相切的性质，涉及的知识有：等边三角形的判定与性质，以及勾股定理，利用了数形结合的思想，其中根据题意得出这堆钢管的层数是解本题的关键．