
【题目】如图9,正方形![]() 的面积为4,反比例函数(
的面积为4,反比例函数(![]() )的图象经过点.
)的图象经过点.
(1) 求点B的坐标和![]() 的值;
的值;
(2) 将正方形分别沿直线![]() 、翻折,得到正方形
、翻折,得到正方形![]() 、.设线段
、.设线段![]() 、分别与函数
、分别与函数![]() ()的图象交于点
()的图象交于点![]() 、,求直线EF的解析式.
、,求直线EF的解析式.

【答案】(1)4;(2)![]()
【解析】试题分析:(1)由正方形的面积公式可求出点B的坐标,将点B的坐标代入反比例函数关系式中可得出关于k的一元一次方程,解方程即可得出结论;
(2)由翻折的性质可得出点E的横坐标、点F的纵坐标,由E、F点在反比例函数上可得出E、F点的坐标,设出直线EF解析式为y=mx+n,由待定系数法即可求出直线EF的解析式.
试题解析:(1)∵正方形OABC的面积为4,
∴OA=OC=2,
∴点B坐标为(2,2).
∵y=![]() 的图象经过点B,
的图象经过点B,
∴k=xy=2×2=4.
(2)∵正方形AMC′B、CBA′N由正方形OABC翻折所得,
∴ON=OM=2OA=4,
∴点E横坐标为4,点F纵坐标为4.
∵点E、F在函数y=![]() 的图象上,
的图象上,
∴当x=4时,y=1,即E(4,1);
当y=4时,x=1,即F(1,4).
设直线EF解析式为y=mx+n,将E、F两点坐标代入,
得![]() ,
,
∴m=-1,n=5.
∴直线EF解析式为y=-x+5.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() m2-n(mn2)2;
m2-n(mn2)2;
(2)(x2-2x)(2x+3)÷(2x);
(3)(2x+y)(2x-y)+(x+y)2-2(2x2+xy);
(4)(ab-b2)÷![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习掷硬币的概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是![]() ”,小明做了下列三个模拟实验来验证.
”,小明做了下列三个模拟实验来验证.
①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值;
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值;
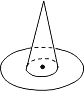
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如图),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值. 上面的实验中,不科学的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图即表示此时小明和小丽的位置.

(1)请画出此时小丽在阳光下的影子;
(2)若已知小明的身高为1.60 m,小明和小丽之间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.
查看答案和解析>>
科目:初中数学 来源: 题型:
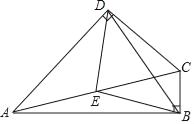
【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点.(1)求证:△BED是等腰三角形:
(2)当∠BCD=_____°时,△BED是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
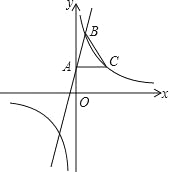
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=![]() (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
(1)求反比例函数的表达式.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
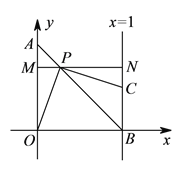
【题目】如图,以![]() 为原点的直角坐标系中,
为原点的直角坐标系中,![]() 点的坐标为
点的坐标为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .点
.点![]() 为线段
为线段![]() 上一动点,作直线
上一动点,作直线![]() ,交直线
,交直线![]() 于点
于点![]() .过
.过![]() 点作直线
点作直线![]() 平行于
平行于![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .记
.记![]() ,
,![]() 的面积为
的面积为![]() .
.
(![]() )当点
)当点![]() 在第一象限时:求证:
在第一象限时:求证:![]() ≌
≌![]() .
.
(![]() )当点
)当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 也随之在直线
也随之在直线![]() 上移动,求出
上移动,求出![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围.
之间的函数关系式,并写出自变量的取值范围.
(![]() )当点
)当点![]() 在线段
在线段![]() 上移动时,
上移动时,![]() 是否可能成为等腰三角形?如果可能,直接写出所有能使
是否可能成为等腰三角形?如果可能,直接写出所有能使![]() 成为等腰三角形的
成为等腰三角形的![]() 的值;如果不可能,请说明理由.
的值;如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
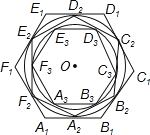
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com