
 的图象上,另“7”字形有两个顶点落在x轴上,一个顶点落在y轴上.
的图象上,另“7”字形有两个顶点落在x轴上,一个顶点落在y轴上.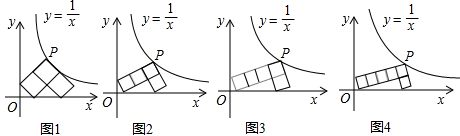
 (1)作PA⊥y轴于A,图中的“7”字形与坐标轴的交点分别为B、C、D,如图1,
(1)作PA⊥y轴于A,图中的“7”字形与坐标轴的交点分别为B、C、D,如图1,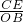 =
=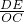 ,
,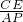 =
= ,
, =
= =
=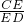 =
= =1,
=1,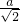 ,
,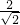 a,
a,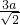 ,
,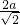 ,
,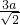 ),
),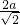 •
•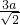 =1,
=1, ;
;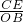 =
=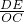 ,
,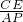 =
= ,
, =
= =
=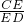 =
= =2,
=2,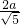 ,
,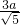 ,AP=
,AP=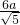
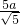 ,
,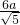 ,
,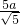 ),
),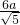 •
•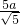 =1,
=1, ;
;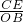 =
=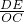 ,
,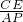 =
= ,
, =
= =
=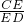 =
=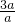 =3,
=3,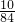 ;
;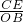 =
=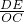 ,
,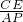 =
= ,
, =
= =
=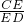 =
=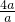 =4,
=4,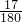 ;
; =
=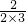 =
=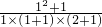 ;
; =
=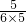 =
=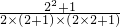 ;
;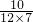 =
=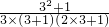 ;
;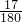 =
=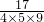 =
=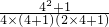 ,
,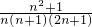 .
. ;(2)
;(2)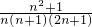 .
. =
= =
=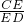 =
= =1,再分别在在RtOBC和Rt△ABP中,利用勾股定理得到OB=
=1,再分别在在RtOBC和Rt△ABP中,利用勾股定理得到OB=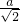 ,AB=AP=
,AB=AP=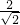 a,则P点坐标为(
a,则P点坐标为(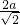 ,
,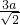 ),然后把P点坐标代入反比例函数解析式得到a2=
),然后把P点坐标代入反比例函数解析式得到a2= ;
;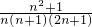 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| n2+1 |
| n(n+1)(2n+1) |
| n2+1 |
| n(n+1)(2n+1) |

查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省成都市高新区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图1~4所示,每个图中的“7”字形是由若干个边长相等的正方形拼接而成,“7”字形的一个顶点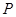 落在反比例函数
落在反比例函数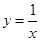 的图像上,另“7”字形有两个顶点落在
的图像上,另“7”字形有两个顶点落在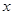 轴上,一个顶点落在
轴上,一个顶点落在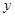 轴上.
轴上.
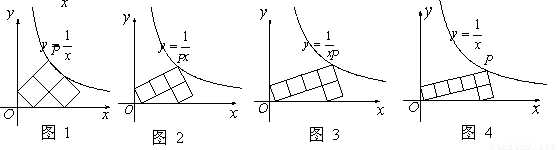
(1)图1中的每一个小正方形的面积是 ;
(2)按照图1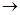 图2
图2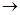 图3
图3 图4
图4
 这样的规律拼接下去,第
这样的规律拼接下去,第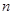 个图形中每一个小正方形的面积是
.(用含
个图形中每一个小正方形的面积是
.(用含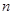 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源:湖北省中考真题 题型:解答题
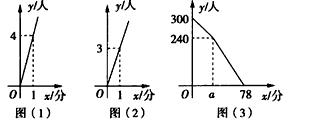
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com