
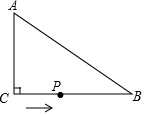
 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.
如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形. 分析 由于没有说明哪一条边是腰,故需要分情况讨论.
解答 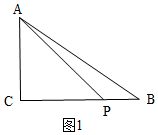 解:∵AC=6,BC=8,
解:∵AC=6,BC=8,
∴由勾股定理可知:AB=10,
当点P在CB上运动时,
由于∠ACP=90°,
∴只能有AC=CP,如图1,
∴CP=6,
∴t=$\frac{6}{2}$=3,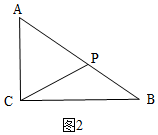
当点P在AB上运动时,
①AC=AP时,如图2,
∴AP=6,PB=AB-CP=10-6=4,
∴t=$\frac{8+4}{2}$=6,
②当AP=CP时,如图3,
此时点P在线段AC的垂直平分线上,
过点P作PD⊥AC于点D,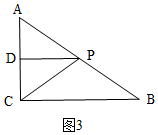
∴CD=$\frac{1}{2}$AC=3,PD是△ACB的中位线,
∴PD=$\frac{1}{2}$BC=4,
∴由勾股定理可知:AP=5,
∴PB=5,
∴t=$\frac{8+5}{2}$=6.5;
③AC=PC时,如图4,
过点C作CF⊥AB于点F,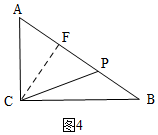
∴cos∠A=$\frac{AC}{AB}$=$\frac{AF}{AC}$,
∴AF=3.6,
∴AP=2AF=7.2,
∴PB=10-7.2=2.8,
∴t=$\frac{8+2.8}{2}$=5.4;
综上所述,当t为3或6或6.5或5.4时,△ACP是等腰三角形.
故答案为:3或6或6.5或5.4.
点评 本题考查等腰三角形的性质,解题的关键是根据腰的情况进行分类讨论,本题属于中等题型.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
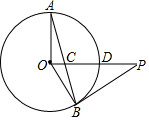
 如图,反比例函数y=$\frac{k}{x}$的图象经过点(-$\sqrt{2}$,-4),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.在点A运动过程中,当BP平分∠ABC时,点C的坐标是(2$\sqrt{2}$,-2).
如图,反比例函数y=$\frac{k}{x}$的图象经过点(-$\sqrt{2}$,-4),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.在点A运动过程中,当BP平分∠ABC时,点C的坐标是(2$\sqrt{2}$,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
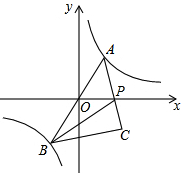
 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
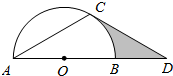
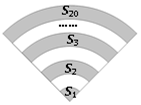 手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=195π.
手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=195π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.5×1010 | B. | 3.5×109 | C. | 3.5×108 | D. | 3.5×107 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com