
 ��ͼ��ijУ�ۺ�ʵ���С���ͬѧ����������һ����DE�ĸ߶ȣ��������������ǰ��һ��¥ͤǰ��̨����A�㴦���������D������Ϊ30�㣬����������ķ����ߵ�̨���µĵ�C�������������D������Ϊ60�㣮��֪A��ĸ߶�ABΪ2m��̨��AC���¶�Ϊ1��$\sqrt{3}$����B��C��E������ͬһ��ֱ���ϣ����������������
��ͼ��ijУ�ۺ�ʵ���С���ͬѧ����������һ����DE�ĸ߶ȣ��������������ǰ��һ��¥ͤǰ��̨����A�㴦���������D������Ϊ30�㣬����������ķ����ߵ�̨���µĵ�C�������������D������Ϊ60�㣮��֪A��ĸ߶�ABΪ2m��̨��AC���¶�Ϊ1��$\sqrt{3}$����B��C��E������ͬһ��ֱ���ϣ�������������������� ��1�������¶������ACB�Ķ������ݴ˼������AC�ij���
��2������AF��DE��F�����ı���ABEFΪ���Σ���DE=x����Rt��CDE�У�CE=$\frac{DE}{��DCE}$=$\frac{DE}{tan60��}$=$\frac{\sqrt{3}}{3}$x����Rt��ABC�У��õ�$\frac{AB}{BC}$=$\frac{1}{\sqrt{3}}$����Rt��AFD�У����x�ij���
��� �⣺��1����̨��AC���¶�Ϊ1��$\sqrt{3}$��
��tan��ACB=$\frac{1}{\sqrt{3}}$��
��tan��ACB=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$��
���ACB=30�㣬
��AC=4m��
��2����ͼ������AF��DE��F�����ı���ABEFΪ���Σ�
��AF=BE��EF=AB=2��
��DE=x����Rt��CDE��CE=$\frac{DE}{��DCE}$=$\frac{DE}{tan60��}$=$\frac{\sqrt{3}}{3}$x��
��Rt��ABC��
��$\frac{AB}{BC}$=$\frac{1}{\sqrt{3}}$��
AB=2��
��BC=2$\sqrt{3}$��
��Rt��AFD��DF=DE-EF=x-2��
��AF=$\frac{DF}{tan��DAF}$=$\frac{x-2}{tan30��}$=$\sqrt{3}$��x-2����
��AF=BE=BC+CE��
��$\sqrt{3}$��x-2��=2$\sqrt{3}$+$\frac{\sqrt{3}}{3}$x��
���x=6��
����DE�ĸ߶�Ϊ6�ף�
���� ���⿼���˽�ֱ�������ε�Ӧ��--���Ǹ������⣬Ҫ��ѧ���ܽ������ǹ���ֱ�������β���ֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ����ABC�ڽ��ڡ�O������B����O�����ߣ���CA���ӳ����ڵ�E����EBC=2��C��
��֪����ͼ����ABC�ڽ��ڡ�O������B����O�����ߣ���CA���ӳ����ڵ�E����EBC=2��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
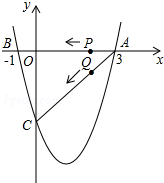 ��ͼ�����κ���y=$\frac{4}{3}$x2+bx+c��ͼ����x�ύ��A��3��0����B��-1��0������y�ύ�ڵ�C������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
��ͼ�����κ���y=$\frac{4}{3}$x2+bx+c��ͼ����x�ύ��A��3��0����B��-1��0������y�ύ�ڵ�C������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2��x3=x2 | B�� | ��-2x��3=-6x3 | C�� | 2x2-x=x | D�� | ��x3��3=x9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
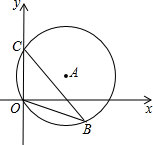 ��ͼ��ֱ��Ϊ10�ġ�A�Ͼ�����C��0��5���͵�0��0��0����B��y���Ҳ��A�Ż���һ�㣬���OBC������ֵΪ��������
��ͼ��ֱ��Ϊ10�ġ�A�Ͼ�����C��0��5���͵�0��0��0����B��y���Ҳ��A�Ż���һ�㣬���OBC������ֵΪ��������| A�� | $\frac{1}{2}$ | B�� | $\frac{3}{4}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com