
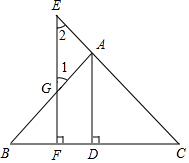
 根据下列证明过程填空:
根据下列证明过程填空:分析 根据等腰三角形的性质得出∠E=∠AGE,根据AD⊥BC,EF⊥BC推出AD∥EF,根据平行线的性质得出∠AGE=∠DAB,∠E=∠DAC,推出∠DAB=∠DAC即可.
解答 证明:∵AD⊥BC,EF⊥BC,
∴∠ADC=∠EFC=90°,
∴AD∥EF,(平面内,垂直于同一条直线的两直线平行)
∴∠AGE=∠DAB,∠E=∠DAC,
∵AE=AG,
∴∠E=∠AGE,
∴∠DAB=∠DAC,
即AD平分∠BAC.
故答案为:平面内,垂直于同一条直线的两直线平行,∠1,∠BAD,∠2,两直线平行,同位角相等,∠1=∠2,∠BAD=∠CAD,角平分线定义.
点评 本题考查了等腰三角形的性质,垂直定义,平行线的性质和判定,主要考查学生的推理能力.


科目:初中数学 来源: 题型:选择题
 如图,用四个螺丝将四条不可弯曲的木条围成一个木框(形状不限),不计螺丝大小,其中相邻两螺丝的距离依次为3、4、5、7,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )
如图,用四个螺丝将四条不可弯曲的木条围成一个木框(形状不限),不计螺丝大小,其中相邻两螺丝的距离依次为3、4、5、7,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com