
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŌŚĖıߊĪABCDÖŠ£¬AB”ĪCD£¬”ĻB=90”ć£¬AB=2CD£®¶ÆµćP“ÓµćA³ö·¢£¬ŌŚĖıߊĪABCDµÄ±ßÉĻŃŲA”śB”śCµÄ·½ĻņŅŌ1cm/sµÄĖŁ¶ČŌČĖŁŅĘ¶Æ£¬µ½“ļµćCŹ±Ķ£Ö¹ŅĘ¶Æ”£ŅŃÖŖ”÷APDµÄĆ껿S(cm 2)ÓėµćPŌĖ¶ÆµÄŹ±¼ät(s)Ö®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼¢ŚĖłŹ¾£¬øł¾ŻĢāŅā½ā“šĻĀĮŠĪŹĢā
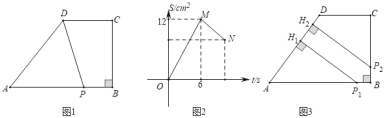
(1)ŌŚĶ¼¢ŁÖŠ£¬AB=”” ””””cm£¬ BC=”” ”” ””cm£®
(2)ĒóĶ¼2ÖŠĻ߶ĪMNµÄŗÆŹż¹ŲĻµŹ½(²¢Š“³ötµÄȔֵ·¶Ī§) £®
(3)ČēĶ¼¢Ū£¬Éč¶ÆµćPÓĆĮĖt1 (s)µ½“ļµćP1“¦£¬ÓĆĮĖt2 (s)µ½“ļµćP2“¦£¬·Ö±š¹żP1”¢P2×÷ADµÄ“¹Ļߣ¬“¹×ćĪŖH1”¢H2£®µ±P1H1= P2H2=4Ź±£¬Į¬P1P2£¬Ēó”÷BP1P2µÄĆ껿£®
”¾“š°ø”æ£Ø1£©6£¬4£»£Ø2£©![]() £Ø6”Üt”Ü10£©£»£Ø3£©
£Ø6”Üt”Ü10£©£»£Ø3£©![]()
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāŗĶĶ¼ĻóæÉÖŖAB=6cm£¬øł¾ŻĶ¼ĻóæÉÖŖ”÷ABDµÄĆ껿ĪŖ12£¬øł¾ŻAB=2CDæɵƔ÷BCDµÄĆ껿£¬ŌŁøł¾ŻĢŻŠĪµÄĆ껿¹«Ź½¼“æÉµĆ³öBCµÄ³¤£»
£Ø2£©øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½Ēó³öµćNµÄ×ų±ź£¬Č»ŗóĄūÓĆ“ż¶ØĻµŹż·Ø£¬¼“æÉĒó³ö½āĪöŹ½£»
£Ø3£©ÓÉ£Ø2£©æÉÖŖ£¬”÷APDµÄĆ껿S£Øcm2£©ÓėµćPŌĖ¶ÆµÄŹ±¼ät£Øs£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬Č»ŗóøł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½½ā“š¼“æÉ£®
½ā£ŗ£Ø1£©øł¾ŻĢāŅāŗĶĶ¼ĻóæÉÖŖAB=6cm£¬BCŹĒĮ½Ę½ŠŠĻߵľąĄė£¬
”ßS”÷ABD£½![]() ABBC£½
ABBC£½![]() ”Į6”ĮBC£½12cm2£®
”Į6”ĮBC£½12cm2£®
”ąBC=4cm£®
¹Ź“š°øĪŖ£ŗ6£»4£»
£Ø2£©µ±µćPŌĖ¶Æµ½µćCŹ±t£½10£¬
”ß![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬
”ąS”÷APD£½![]() £¬
£¬
”ąN(10£¬6)£¬
ÉčĻ߶ĪMNµÄ½āĪöŹ½ĪŖ£ŗs£½at+b£¬
°ŃM(6£¬12)N(10£¬6)“śČėµĆ£ŗ
![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ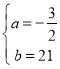 £¬
£¬
”ą![]() £Ø6”Üt”Ü10£©£»
£Ø6”Üt”Ü10£©£»
£Ø3£©¹żµćD×÷DE”ĶAB£¬“¹×ćĪŖE£¬
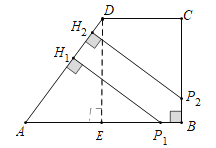
”ßDE£½BC£½4£¬AE£½AB©BE£½AB©CD£½3£¬
”ą![]() £¬
£¬
”ßµ±µćPŌŚAB±ßÉĻ£¬¼“0”Üt”Ü6Ź±£¬S£½2t£»
µ±µćPŌŚBC±ßÉĻ£¬¼“6”Üt”Ü10Ź±£¬![]() £¬
£¬
”ßP1H1£½P2H2£½4£¬
”ą![]() £¬¼“2t£½10£¬
£¬¼“2t£½10£¬
½āµĆ£ŗt1£½5£»
”ą![]() £¬¼“
£¬¼“![]() £¬
£¬
½āµĆ£ŗt2£½![]() £¬
£¬
”ą![]() ”Į(6£5) ”Į(
”Į(6£5) ”Į(![]() £6)£½
£6)£½![]() .
.


 æŚĖćĢāæؼÓÓ¦ÓĆĢā¼ÆѵĻµĮŠ“š°ø
æŚĖćĢāæؼÓÓ¦ÓĆĢā¼ÆѵĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
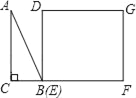
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCĪŖÖ±½ĒČż½ĒŠĪ£¬”ĻC=90”ć£¬BC=2cm£¬”ĻA=30”ć£¬ĖıߊĪDEFGĪŖ¾ŲŠĪ£¬DE=2![]() cm£¬EF=6cm£¬ĒŅµćC”¢B”¢E”¢FŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬µćBÓėµćEÖŲŗĻ£®Rt”÷ABCŅŌĆæĆė1cmµÄĖŁ¶ČŃŲ¾ŲŠĪDEFGµÄ±ßEFĻņÓŅĘ½ŅĘ£¬µ±µćCÓėµćFÖŲŗĻŹ±Ķ£Ö¹£®ÉčRt”÷ABCÓė¾ŲŠĪDEFGµÄÖŲµž²æ·ÖµÄĆ껿ĪŖycm2£¬ŌĖ¶ÆŹ±¼äxs£®ÄÜ·“Ó³ycm2ÓėxsÖ®¼äŗÆŹż¹ŲĻµµÄ“óÖĀĶ¼ĻóŹĒ£Ø””””£©
cm£¬EF=6cm£¬ĒŅµćC”¢B”¢E”¢FŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬µćBÓėµćEÖŲŗĻ£®Rt”÷ABCŅŌĆæĆė1cmµÄĖŁ¶ČŃŲ¾ŲŠĪDEFGµÄ±ßEFĻņÓŅĘ½ŅĘ£¬µ±µćCÓėµćFÖŲŗĻŹ±Ķ£Ö¹£®ÉčRt”÷ABCÓė¾ŲŠĪDEFGµÄÖŲµž²æ·ÖµÄĆ껿ĪŖycm2£¬ŌĖ¶ÆŹ±¼äxs£®ÄÜ·“Ó³ycm2ÓėxsÖ®¼äŗÆŹż¹ŲĻµµÄ“óÖĀĶ¼ĻóŹĒ£Ø””””£©
A. 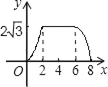 B.
B. 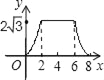 C.
C. 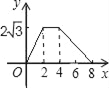 D.
D. 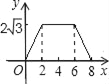
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶ¼1ŹĒŅ»ĢØŹµĪļĶ¶Ó°ŅĒ£¬Ķ¼2ŹĒĖüµÄŹ¾ŅāĶ¼£¬ÕŪĻß![]() ±ķŹ¾¹Ģ¶ØÖ§¼Ü£¬
±ķŹ¾¹Ģ¶ØÖ§¼Ü£¬![]() “¹Ö±Ė®Ę½×ĄĆę
“¹Ö±Ė®Ę½×ĄĆę![]() £¬µć
£¬µć![]() ĪŖŠż×Ŗµć£¬
ĪŖŠż×Ŗµć£¬![]() æÉŅŌŠż×Ŗ£¬µ±
æÉŅŌŠż×Ŗ£¬µ±![]() Čʵć
Čʵć![]() ÄꏱÕėŠż×ŖŹ±£¬Ķ¶Ó°Ģ½Ķ·
ÄꏱÕėŠż×ŖŹ±£¬Ķ¶Ó°Ģ½Ķ·![]() Ź¼ÖÕ“¹Ö±ÓŚĖ®Ę½×ĄĆę
Ź¼ÖÕ“¹Ö±ÓŚĖ®Ę½×ĄĆę![]() £¬¾²āĮæ£ŗ
£¬¾²āĮæ£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £®(½į¹ū¾«Č·µ½
£®(½į¹ū¾«Č·µ½![]() )
)
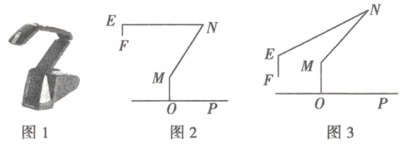
(1)ČēĶ¼2ĖłŹ¾£¬![]() £¬
£¬![]() .
.
¢ŁĢīæÕ£ŗ![]() £»
£»
¢ŚĒóĶ¶Ó°Ģ½Ķ·µÄ¶Ėµć![]() µ½×ĄĆę
µ½×ĄĆę![]() µÄ¾ąĄė£»
µÄ¾ąĄė£»
(2)ČēĶ¼3ĖłŹ¾£¬½«(1)ÖŠµÄ![]() ĻņĻĀŠż×Ŗ£¬µ±Ķ¶Ó°Ģ½Ķ·µÄ¶Ėµć
ĻņĻĀŠż×Ŗ£¬µ±Ķ¶Ó°Ģ½Ķ·µÄ¶Ėµć![]() µ½×ĄĆę
µ½×ĄĆę![]() µÄ¾ąĄėĪŖ
µÄ¾ąĄėĪŖ![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄ“󊔣®(²Īæ¼Źż¾Ż
µÄ“󊔣®(²Īæ¼Źż¾Ż![]() span>)
span>)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬PĪŖ”ŃOÖ±¾¶ABŃÓ³¤ĻßÉĻµÄŅ»µć£¬PCĒŠ”ŃOÓŚµćC£¬¹żµćB×÷CPµÄ“¹ĻßBH½»”ŃOÓŚµćD£¬Į¬½įAC£¬CD£®
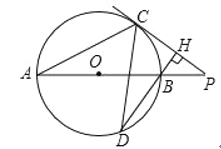
£Ø1£©ĒóÖ¤£ŗ”ĻPBH£½2”ĻHDC£»
£Ø2£©Čōsin”ĻP£½![]() £¬BH£½3£¬ĒóBDµÄ³¤£®
£¬BH£½3£¬ĒóBDµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
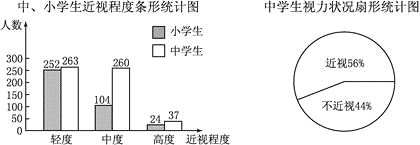
”¾ĢāÄæ”æijŹŠĒąÉŁÄź½”æµŃŠ¾æÖŠŠÄĖ껜³éČ”ĮĖ±¾ŹŠ1000ĆūŠ”ѧɜŗĶČōøÉĆū֊ѧɜ£¬¶ŌĖūĆĒµÄŹÓĮ¦×“æö½ųŠŠĮĖµ÷²é£¬²¢°Ńµ÷²é½į¹ū»ęÖĘ³ÉČēĻĀĶ³¼ĘĶ¼.£Ø½üŹÓ³Ģ¶Č·ÖĪŖĒį¶Č”¢ÖŠ¶Č”¢ø߶ČČżÖÖ£©
£Ø1£©ĒóÕā1000ĆūŠ”ѧɜ»¼½üŹÓµÄ°Ł·Ö±Č.
£Ø2£©Ē󱾓Ī³é²éµÄ֊ѧɜČĖŹż.
£Ø3£©øĆŹŠÓŠÖŠŃ§Éś8ĶņČĖ£¬Š”ѧɜ10ĶņČĖ.·Ö±š¹Ą¼ĘøĆŹŠµÄ֊ѧɜÓėŠ”ѧɜ»¼”°ÖŠ¶Č½üŹÓ”±µÄČĖŹż.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖŌöĒæѧɜµÄ°²Č«ŅāŹ¶£¬ĪŅŹŠÄ³ÖŠŃ§×éÖƳõȿğ¼¶1000Ćūѧɜ²Ī¼ÓĮĖ”°Š£Ō°°²Č«ÖŖŹ¶¾ŗČü”±£¬Ė껜³éČ”ĮĖŅ»øö°ąŃ§ÉśµÄ³É¼Ø½ųŠŠÕūĄķ£¬·ÖĪŖ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ĖÄøöµČ¼¶£¬²¢°Ń½į¹ūÕūĄķ»ęÖĘ³ÉĢõŠĪĶ³¼ĘĶ¼ÓėÉČŠĪĶ³¼ĘĶ¼£Ø²æ·Ö£©£¬ĒėŅĄ¾ŻČēĶ¼Ģį¹©µÄŠÅĻ¢£¬Ķź³ÉĻĀĮŠĪŹĢā£ŗ
ĖÄøöµČ¼¶£¬²¢°Ń½į¹ūÕūĄķ»ęÖĘ³ÉĢõŠĪĶ³¼ĘĶ¼ÓėÉČŠĪĶ³¼ĘĶ¼£Ø²æ·Ö£©£¬ĒėŅĄ¾ŻČēĶ¼Ģį¹©µÄŠÅĻ¢£¬Ķź³ÉĻĀĮŠĪŹĢā£ŗ
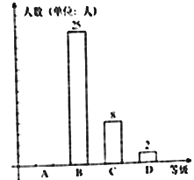
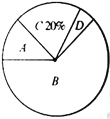
£Ø1£©Ēė¹Ą¼Ę±¾Š£³õȿğ¼¶µČ¼¶ĪŖ![]() µÄѧɜČĖŹż£»
µÄѧɜČĖŹż£»
£Ø2£©Ń§Š£¾ö¶Ø“ÓµĆĀś·ÖµÄ3ĆūÅ®ÉśŗĶ2ĆūÄŠÉśÖŠĖ껜³éČ”3ČĖ²Ī¼ÓŹŠ¼¶±ČČü£¬ĒėĒó³öĒ”ŗĆ³éµ½2ĆūÅ®ÉśŗĶ1ĆūÄŠÉśµÄøÅĀŹ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹß²Ė¾ĻśÉĢČ„Źß²ĖÉś²ś»łµŲÅś·¢Ä³ÖÖŹß²Ė£¬ŅŃÖŖÕāÖÖŹß²ĖµÄÅś·¢ĮæŌŚ20Ē§æĖÖĮ60Ē§æĖÖ®¼ä£Øŗ¬20Ē§æĖŗĶ60Ē§æĖ£©Ź±£¬ĆæĒ§æĖÅś·¢5ŌŖ£»Čō³¬¹ż60Ē§æĖŹĒ£¬Åś·¢µÄÕāÖÖŹß²ĖČ«²æ“ņ°ĖÕŪ£¬µ«Åś·¢×ܽš¶ī²»µĆÉŁÓŚ300ŌŖ£®
£Ø1£©øł¾ŻĢāŅā£¬ĢīŠ“Čē±ķ£ŗ
Źß²ĖµÄÅś·¢Įæ£ØĒ§æĖ£© | ... | 25 | 60 | 75 | 90 | ... |
Ėłø¶µÄ½š¶ī£ØŌŖ£© | ... | 125 | 300 | ... |
£Ø2£©¾µ÷²é£¬øĆŹß²Ė¾ĻśÉĢĻśŹŪøĆÖÖŹß²ĖµÄČÕĻśŹŪĮæ![]() £ØĒ§æĖ£©ÓėĮćŹŪ¼Ūx£ØŌŖ/Ē§æĖ£©ŹĒŅ»“ĪŗÆŹż¹ŲĻµ£¬ĘäĶ¼ĻóČēĶ¼£¬Ēó³ö
£ØĒ§æĖ£©ÓėĮćŹŪ¼Ūx£ØŌŖ/Ē§æĖ£©ŹĒŅ»“ĪŗÆŹż¹ŲĻµ£¬ĘäĶ¼ĻóČēĶ¼£¬Ēó³ö![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
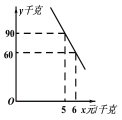
£Ø3£©ČōøĆŹß²Ė¾ĻśÉĢĆæČÕĻśŹŪ“ĖÖÖŹß²Ė²»µĶÓŚ75Ē§æĖ£¬ĒŅĮćŹŪ¼Ū²»±ä£¬ÄĒĆ“ĮćŹŪ¼Ū¶ØĪŖ¶ąÉŁŹ±£¬øĆ¾ĻśÉĢĻśŹŪ“ĖÖÖŹß²ĖµÄµ±ČÕĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
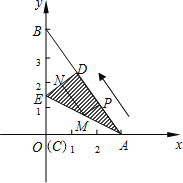
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬Rt”÷ABCŹĒŅ»ÕÅ·ÅŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠµÄÖ½Ę¬£¬µćCÓėŌµćOÖŲŗĻ£¬µćAŌŚxÖįµÄÕż°ėÖįÉĻ£¬µćBŌŚyÖįµÄÕż°ėÖįÉĻ£¬ŅŃÖŖOA=3£¬OB£½4.½«Ö½Ę¬µÄÖ±½Ē²æ·Ö·ÕŪ£¬Ź¹µćCĀäŌŚAB±ßÉĻ£¬¼ĒĪŖDµć£¬AEĪŖÕŪŗŪ£¬EŌŚyÖįÉĻ.
£Ø1£©ŌŚĻĀĶ¼ĖłŹ¾µÄÖ±½Ē×ų±źĻµÖŠ£¬ĒóEµćµÄ×ų±ź¼°AEµÄ³¤.
£Ø2£©Ļ߶ĪADÉĻÓŠŅ»¶ÆµćP£Ø²»ÓėA”¢DÖŲŗĻ£©×ŌAµćŃŲAD·½ĻņŅŌĆæĆė1øöµ„Ī»³¤¶ČĻņDµć×÷ŌČĖŁŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£Ø0<t<3£©£¬¹żPµć×÷PM”ĪDE½»AEÓŚMµć£¬¹żµćM×÷MN”ĪAD½»DEÓŚNµć£¬ĒóĖıߊĪPMNDµÄĆ껿SÓėŹ±¼ätÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬µ±tČ”ŗĪÖµŹ±£¬SÓŠ×ī“óÖµ£æ×ī“óÖµŹĒ¶ąÉŁ£æ
£Ø3£©µ±t£Ø0<t<3£©ĪŖŗĪÖµŹ±£¬A”¢D”¢MČżµć¹¹³ÉµČŃüČż½ĒŠĪ£æ²¢Ēó³öµćMµÄ×ų±ź.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ“Ł½ųѧɜ¶ąŃł»Æ·¢Õ¹£¬Ä³Š£×éÖÆæŖÕ¹ĮĖÉēĶÅ»ī¶Æ£¬·Ö±šÉčÖĆĮĖĢåÓżĄą”¢ŅÕŹõĄą”¢ĪÄѧĄą¼°ĘäĖüĄąÉēĶÅ£ØŅŖĒóČĖČĖ²ĪÓėÉēĶÅ£¬ĆæČĖÖ»ÄÜŃ”ŌńŅ»Ļī£©£®ĪŖĮĖ½āѧɜĻ²°®ÄÄÖÖÉēĶÅ»ī¶Æ£¬Ń§Š£×öĮĖŅ»“Ī³éŃłµ÷²é£®øł¾ŻŹÕ¼Æµ½µÄŹż¾Ż£¬»ęÖĘ³ÉČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬Ēėøł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢£¬Ķź³ÉĻĀĮŠĪŹĢā£ŗ

£Ø1£©“Ė“Ī¹²µ÷²éĮĖ¶ąÉŁČĖ£æ
£Ø2£©ĒóĪÄѧÉēĶÅŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠĖłÕ¼Ō²ŠÄ½ĒµÄ¶ČŹż£»
£Ø3£©Ēė½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø4£©ČōøĆŠ£ÓŠ1500Ćūѧɜ£¬Ēė¹Ą¼ĘĻ²»¶ĢåÓżĄąÉēĶŵÄѧɜӊ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com