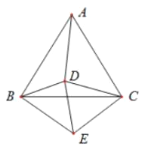
【题目】如图，已知正三角形ABC与正三角形CDE，若∠DBE=66°，则∠ADB度数为__________.
【答案】126°
【解析】
现根据正三角形ABC与正三角形CDE证出△BCE
△ADC，从而得出∠ADC=∠BEC∠BED+60°;再根据三角形的内角和得出∠BDE=114°-∠BED，再根据∠ADB=360°-∠ADC-∠BDE-∠EDC即可得出∠ADB的度数。
∵正三角形ABC与正三角形CDE
∴CD=CE,BC=AC, ∠DEC=∠EDC=∠DCE=60°
∴∠EDC-∠BCD=∠DCE-∠BCD
∴∠BCE=∠DCA
在△BCE和△ADC中;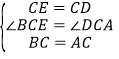
∴△BCE△ADC ∴∠ADC=∠BEC;
∵∠BEC=∠BED+∠DEC=∠BED+60°;
∴∠ADC=∠BED+60°
在△BDE中，∠BDE=180°-∠DBE-∠BED=180°-66°-∠BED=114°-∠BED
∴∠ADB=360°-∠ADC-∠BDE-∠EDC=360°-（∠BED+60°）-（114°-∠BED）-60°=126°
故答案为：126°
科目：初中数学 来源： 题型：
【题目】已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．
①画出△ABC向上平移6个单位得到的△A1B1C1；
②以点C为位似中心，在网格中画出△A2B2C2 ， 使△A2B2C2与△ABC位似，且△A2B2C2与△ABC的位似比为2：1，并直接写出点A2的坐标
查看答案和解析>>
科目：初中数学 来源： 题型：
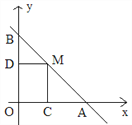
【题目】如图，直线y=4－x与两坐标轴分别相交于A、B点，点M是线段AB上任意一点(A、B两点除外)，过M分别作MC⊥OA于点C，MD⊥OB于点D。
(1)当点M在AB上运动时，四边形OCMD的周长为________；
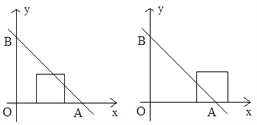
(2)当四边形OCMD为正方形时，将正方形OCMD沿着x轴的正方向移动，设平移的距离为a (0<a≤4)，在平移过程中：
①当平移距离a=1时, 正方形OCMD与△AOB重叠部分的面积为________；
②当平移距离a是多少时，正方形OCMD的面积被直线AB分成l：3两个部分?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：两直线l1，l2满足l1∥l2 ，点C，点D在直线l1上，点A，点B在直线l2上，点P是平面内一动点，连接CP，BP，
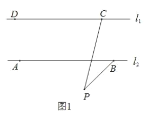
（1）如图 1，若点P在 l1，l2外部，则∠DCP、∠CPB、∠ABP之间满足什么数量关系？请你证明的这个结论；
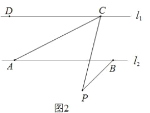
（2）如图 2，若点P在l1，l2外部，连接AC，则∠CAB、∠ACP、∠CPB、∠ABP之间满足什么数量关系？请你证明这个结论；（不能用三角形内角和为 180°）
（3）若点P在 l1，l2内部，且在AC的右侧，则∠ACP﹑∠ABP﹑∠CAB﹑∠CPB之间满足什么数量关系？（不需证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列因式分解的过程：
（1）x2﹣xy+4x﹣4y
＝（x2﹣xy）+（4x﹣4y）（分成两组）
＝x（x﹣y）+4（x﹣y）直接提公因式）
＝（x﹣y）（x+4）
（2）a2﹣b2﹣c2+2bc
＝a2﹣（b2+c2﹣2bc）（分成两组）
＝a2﹣（b﹣c）2（直接运用公式）
＝（a+b﹣c）（a﹣b+c）
（1）请仿照上述分解因式的方法，把下列各式分解因式：
①
②
（2）请运用上述分解因式的方法，把多项式1+x+x（1+x）+x（1+x）2+…+x（1+x）n分解因式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
