练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在正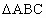内有一点P，PA＝10，PB＝8，PC＝6，则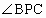的度数为________度．

    答案：150
    提示：

    以C为中心将逆时针旋转60°，得到，则．

    为等边三角形，．

    ∴．

    ∴为直角三角形，．

    ∴．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    （2012•石家庄二模）阅读下列材料：
    问题：如图1，在正方形ABCD内有一点P，PA=
    		5
    ，PB=
    		2
    ，PC=1，求∠BPC的度数．
    小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连接PP′．
    请你参考小明同学的思路，解决下列问题：
    （1）图2中∠BPC的度数为
    135°
    135°
    ；
    （2）如图3，若在正六边形ABCDEF内有一点P，且PA=2
    		13
    ，PB=4，PC=2，则∠BPC的度数为
    120°
    120°
    ，正六边形ABCDEF的边长为
    2
    		7
    2
    		7
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在正方形ABCD内有一点P，PA=
    		5
    ，PB=
    		2
    ，PC=1，求∠BPC的度数．
    【分析问题】根据已知条件比较分散的特点，我们可以通过旋转变换将分散的已知条件集中在一起，于是将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′．
    【解决问题】请你通过计算求出图2中∠BPC的度数；
    【比类问题】如图3，若在正六边形ABCDEF内有一点P，且PA=2
    		13
    ，PB=4，PC=2．
    （1）∠BPC的度数为
    120°
    120°
    ； 
    （2）直接写出正六边形ABCDEF的边长为
    2
    		7
    2
    		7
    ．

    查看答案和解析>>

    科目：初中数学 来源：2013届北京市三十一中学初三上学期期中考试数学试卷（带解析） 题型：解答题

    问题：如图1，在正方形ABCD内有一点P，PA=，PB=，PC=1，求∠BPC的度数．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′．

    请你参考小明同学的思路，解决下列问题：
    (1) 图2中∠BPC的度数为      ；
    (2) 如图3，若在正六边形ABCDEF内有一点P，且PA=，PB=4，PC=2，则∠BPC的度数为       ，正六边形ABCDEF的边长为      ．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年北京市初三上学期期中考试数学试卷（解析版） 题型：解答题

    问题：如图1，在正方形ABCD内有一点P，PA=，PB=，PC=1，求∠BPC的度数．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′．

    请你参考小明同学的思路，解决下列问题：

    (1) 图2中∠BPC的度数为       ；

    (2) 如图3，若在正六边形ABCDEF内有一点P，且PA=，PB=4，PC=2，则∠BPC的度数为        ，正六边形ABCDEF的边长为       ．

     

    查看答案和解析>>

    同步练习册答案