
【题目】把下列各数填在相应的大括号里:
-3,0.2,0,-|+![]() |,-5%,-
|,-5%,-![]() ,|-9|,-(-1),-23,+3
,|-9|,-(-1),-23,+3![]() .
.
(1)正整数集合:{ …};
(2)负分数集合:{ …};
(3)负数集合:{ …};
(4)整数集合:{ …};
(5)分数集合:{ …};
(6)非负数集合:{ …}.
【答案】(1)|-9|,-(-1) (2)-|+![]() |,-5%,-
|,-5%,-![]()
(3)-3,-|+![]() |,-5%,-
|,-5%,-![]() ,-23 (4)-3,0,|-9|,-(-1),-23
,-23 (4)-3,0,|-9|,-(-1),-23
(5)0.2,-|+![]() |,-5%,-
|,-5%,-![]() ,+3
,+3![]() (6)0.2,0,|-9|,-(-1),+3
(6)0.2,0,|-9|,-(-1),+3![]()
【解析】
先对各数进行化简,然后根据有理数的分类即可得出答案.
解:-|+![]() |=-
|=-![]() ,|-9|=9,-(-1)=1,-23=-8,
,|-9|=9,-(-1)=1,-23=-8,
(1)正整数集合:{|-9|,-(-1)…};
(2)负分数集合:{-|+![]() |,-5%,-
|,-5%,-![]() …};
…};
(3)负数集合:{-3,-|+![]() |,-5%,-
|,-5%,-![]() ,-23…};
,-23…};
(4)整数集合:{-3,0,|-9|,-(-1),-23…};
(5)分数集合:{0.2,-|+![]() |,-5%,-
|,-5%,-![]() ,+3
,+3![]() …};
…};
(6)非负数集合:{0.2,0,|-9|,-(-1),+3![]() …}.
…}.


科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上一点,∠BOC=120°,OD平分∠AOC.
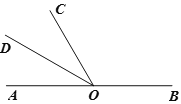
(1)求∠COD的度数.
请你补全下列解题过程.
∵点O为直线AB上一点,
∴∠AOB=_____.
∵∠BOC =120°,
∴∠AOC=______.
∵OD 平分∠AOC,
∴∠COD=![]() ∠AOC.( )
∠AOC.( )
∴∠COD=________.
(2)若E是直线AB外一点,满足∠COE:∠BOE=4:1直接写出∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;其中正确的有( )
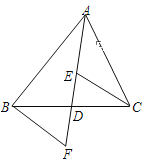
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,D是等边三角形ABC外一点,DB=DC,∠BDC=120°,点E,F分别在AB,AC上.
(1)求证:AD是BC的垂直平分线.
(2)若ED平分∠BEF,求证:FD平分∠EFC.
(3)在(2)的条件下,求∠EDF的度数.
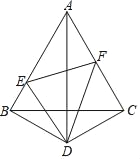
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A在数轴上对应的数为![]() 点B对应的数为
点B对应的数为![]() 且
且![]() 满足
满足![]()
(1)线段AB的长为________;
(2)点C在数轴上对应的数为10,在数轴上是否存在点D,使得DA+DB=DC?若存在,求出点D对应的数;若不存在,说明理由。
(3)动点P从点A出发,以每秒6个单位长度的速度沿数轴向左均速运动;动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左移动;动点M从点A出发,以每秒3个单位长度的速度沿数轴向左均速移动,点P、Q、M同时出发,设运动时间为![]() 秒,当
秒,当![]() 时,探究QP、QA、QM三条线段之间的数量关系,并说明理由.
时,探究QP、QA、QM三条线段之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在商场购买甲、乙两种不同的运动器材,购买甲种器材花费1 500元,购买乙种器材花费1 000元,购买甲种器材数量是购买乙种器材数量的2倍,且购买一件乙种器材比购买一件甲种器材多花10元.
(1)求购买一件甲种器材、一件乙种器材各需多少元?
(2)该中学决定再次购买甲、乙两种运动器材共50件,恰逢该商场对两种运动器材的售价进行调整,甲种器材售价比第一次购买时提高了10%,乙种器材售价比第一次购买时降低了10%,如果此次购买甲、乙两种器材的总费用不超过1 700元,那么这所学校最多可购买多少件乙种器材?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com