
 �����Ҷ���C�ĺ�����Ϊ4����ͼ����x���Ͻص��߶�AB��Ϊ6��
�����Ҷ���C�ĺ�����Ϊ4����ͼ����x���Ͻص��߶�AB��Ϊ6��
 �⣺��1���߶Գ���Ϊֱ��x=4��ͼ����x���Ͻصõ��߶γ�Ϊ6��
�⣺��1���߶Գ���Ϊֱ��x=4��ͼ����x���Ͻصõ��߶γ�Ϊ6�� ����
���� =16a+k�٣�
=16a+k�٣� ��k=-
��k=- ��
�� ��x-4��2-
��x-4��2- ��y=
��y= x2-
x2-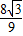 x+
x+ ��
�� ��
�� =
= ��
�� ����
���� +
+ ��
�� ����
����
 ��
�� ��BN=3��ON=10����ʱ��Q��10��3
��BN=3��ON=10����ʱ��Q��10��3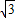 �������AB=AQ���ɶԳ���֪Q��-2��3
�������AB=AQ���ɶԳ���֪Q��-2��3 ��
�� ����
���� ���루-2��3
���루-2��3 �������������ϣ�
�������������ϣ� ����-2��3
����-2��3 ����4��-
����4��- ����
����

 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2011�����ʡ�Ƹ��к찲���п���ѧģ���Ծ��������棩 ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�����ʡ�Ƹ��к찲���п���ѧģ���Ծ��������棩 ���ͣ������
| ͼ������ | Ƶ�� | Ƶ�� |
| ���ճ�ʶ | B | 0.2 |
| ���˴��� | 500 | 0.25 |
| �������� | 800 | A |
| ���� | 300 | 0.15 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�����ʡ�Ƹ��к찲���п���ѧģ���Ծ��������棩 ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�����ʡ�Ƹ��л�÷���п���ѧģ���Ծ���08���������棩 ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com