
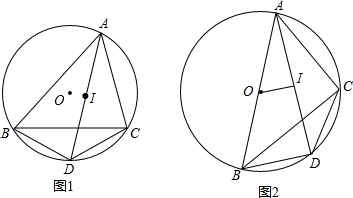
分析 (1)要证明ID=BD=DC,只要求得∠BID=∠IBD,再根据角平分线的性质即可得到结论;
(2)由AB是⊙O的直径,得到BD⊥AD,由于OI⊥AD,得到OI∥BD,于是求得AD=2BD,BD=2OI,设OI=x,则BD=AI=2x,AD=4x,得到AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{5}$x,如图2,过O作OE⊥BD交⊙O于E,连接AE交OI于F,则OE∥AI,得到比例式代入求得IF=$\frac{2}{\sqrt{5}+2}$x,即可得到结果.
解答 (1)证明:∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∴∠BID=∠ABI+∠BAD,
∴∠ABI=∠CBI,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD,
∵∠BAD=∠CAD,
∴$\widehat{BD}=\widehat{CD}$,
∴CD=BD,
∴DB=DC=DI;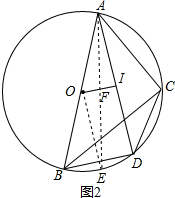
(2)∵AB是⊙O的直径,
∴BD⊥AD,OI⊥AD,
∴OI∥BD,
∵OA=OB,
∴AI=DI,
由(1)知ID=BD,
∴AD=2BD,BD=2OI,
设OI=x,则BD=AI=2x,AD=4x,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{5}$x,
如图2,过O作OE⊥BD交⊙O于E,连接AE交OI于F,则OE∥AI,
∴$\frac{AI}{OE}=\frac{IF}{OF}$,
即$\frac{2x}{\sqrt{5}x}$=$\frac{IF}{x-IF}$,
∴IF=$\frac{2}{\sqrt{5}+2}$x,
∵OE⊥BD,
∴$\widehat{BE}=\widehat{DE}$,
∴∠DAE=$\frac{1}{2}$∠BAD=$\frac{1}{2}$∠CAD,
∴tan∠DAE=tan$\frac{∠CAD}{2}$=$\frac{IF}{AI}=\frac{\frac{2}{\sqrt{5}+2}x}{2x}$=$\sqrt{5}$-2.
点评 本题考查了三角形的内切圆和内心,三角形的外接圆和外心,垂径定理,圆周角定理,三角形外角性质,等腰三角形的判定等知识点的应用,能正确作出辅助线并求出AD=2BD是解此题的关键,有一定的难度.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 2m>2n | B. | m-2>n-2 | C. | -3m>-3n | D. | $\frac{m}{3}$>$\frac{n}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
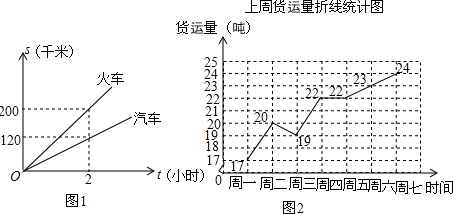
| 运输工具 | 运输费单价:元/(吨•千米) | 冷藏费单价:元/(吨•时) | 固定费用:元/次 |
| 汽车 | 2 | 5 | 200 |
| 火车 | 1.6 | 5 | 2280 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
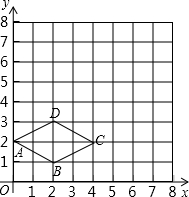 如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.
如图,在平面直角坐标系中,菱形ABCD各顶点均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
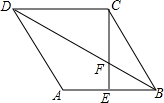 如图,四边形ABCD是菱形,CE⊥AB,垂足为点E,且CE交对角线BD于点F.若∠A=120°,四边形AEFD的面积为$\frac{5\sqrt{3}}{6}$,求EF的值.
如图,四边形ABCD是菱形,CE⊥AB,垂足为点E,且CE交对角线BD于点F.若∠A=120°,四边形AEFD的面积为$\frac{5\sqrt{3}}{6}$,求EF的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
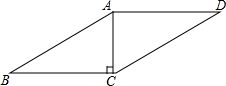 如图,在?ABCD中,过A点作高,垂足刚好为点C,AB=4,AC=2,则?ABCD的周长是( )
如图,在?ABCD中,过A点作高,垂足刚好为点C,AB=4,AC=2,则?ABCD的周长是( )| A. | 8+4$\sqrt{3}$ | B. | 4+2$\sqrt{3}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 周阅读用时数(小时) | 4 | 5 | 8 | 12 |
| 学生人数(人) | 3 | 4 | 2 | 1 |
| A. | 中位数是6.5 | B. | 众数是12 | C. | 平均数是3.9 | D. | 方差是6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com