练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】小毅和小明同时从学校出发到科技馆参加活动，小毅每小时走6千米，小明每小时走8千米，走了1小时后，小明忘带材料返回学校取材料，立即按原路去追小毅．小明几小时追上小毅？

    【答案】小明3小时追上小毅．

    【解析】试题分析：利用小明与小毅的时间差值为1小时，进而根据路程相等列出方程求出即可．

    解：设小明x小时追上小毅，可得：

    8x=6（x+1），

    解得：x=3．

    答：小明3小时追上小毅．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】对于四边形ABCD，给出下列4组条件：①∠A=∠B=∠C=∠D；②∠B=∠C=∠D；③∠A=∠B，∠C=∠D；④∠A=∠B=∠C=90°，其中能得到“四边形ABCD是矩形”的条件有（ ）

    A. 1组 B. 2组 C. 3组 D. 4组

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上A，B两点所表示的数分别是3，﹣2，则表示AB之间距离的算式是（　　）

    A. 3﹣（﹣2） B. 3+（﹣2） C. ﹣2﹣3 D. ﹣2﹣（﹣3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】代数式a+b2的意义是（　　）

    A. a与b的和的平方 B. a与b两数的平方和

    C. a与b的平方的和 D. a与b的平方

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若函数y＝x2+2x﹣m的图象与x轴有且只有一个交点，则m的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人各自加工相同数量的零件，甲先开始工作，中途因故停机检修1小时，重新工作时依旧按照原来的工作效率加工零件，如图是甲、乙两人在整个过程中各自加工的零件个数y（个）与甲工作时间x（时）之间的函数图象．

    （1）图中m= ，a= ．

    （2）求重新工作后甲加工的零件个数y与x之间的函数关系式．

    （3）求乙工作期间两人加工的零件个数相差100个时x的值．

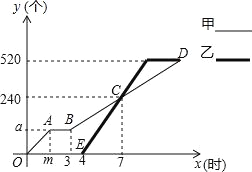
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等腰三角形ABCD中，AB=AC，分别在射线AB、CA上取点D、E，连结DE，过点E作EF∥AB交直线BC于点F，直线BC与DE所在直线交于点M．

    猜想：如图①，点D在边AB延长线上，点E在边AC上，且BD=CE，则线段BM、EM的大小关系为 ．

    探究：如图②，点D、E分别在边AB、CA延长线上，且BD=CE，判断线段DM、EM的大小关系，并加以证明．

    拓展：如图③，点D在边AB上（点D不与点A、B重合），点E在边CA的延长线上，其它条件不变，若BD=1，CE=4，DM=0.7，则线段DE的长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为提高饮水质量，越来越多的居民选购家用净水器．一商场抓住商机，从厂家购进了A、B两种型号家用净水器共160台，A型号家用净水器进价是150元/台，B型号家用净水器进价是350元/台，购进两种型号的家用净水器共用去36000元．

    （1）求A、B两种型号家用净水器各购进了多少台；

    （2）为使每台B型号家用净水器的毛利润是A型号的2倍，且保证售完这160台家用净水器的毛利润不低于11000元，求每台A型号家用净水器的售价至少是多少元．（注：毛利润=售价﹣进价）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列事件是必然事件的是（　　）

    A. 三点确定一个圆 B. 三角形内角和180度

    C. 明天是晴天 D. 打开电视正在放广告

    查看答案和解析>>

    同步练习册答案