试题分析:(1)仔细分析题意根据折叠的性质及“好角”的定义即可作出判断;
(2)因为经过三次折叠∠BAC是△ABC的好角,所以第三次折叠的∠A
2B
2C=∠C,由∠ABB
1=∠AA
1B
1,∠AA
1B
1=∠A
1B
1C+∠C,又∠A
1B
1C=∠A
1A
2B
2,∠A
1A
2B
2=∠A
2B
2C+∠C,∠ABB
1=∠A
1B
1C+∠C=∠A
2B
2C+∠C+∠C=3∠C,由此即可求得结果;
(3)因为最小角是4º是△ABC的好角,根据好角定义,则可设另两角分别为4mº,4mnº(其中m、n都是正整数),由题意得4m+4mn+4=180,所以m(n+1)=44,再根据m、n都是正整数可得 m与n+1是44的整数因子,从而可以求得结果.
(1)由题意得∠BAC是△ABC的好角;
(2)因为经过三次折叠∠BAC是△ABC的好角,所以第三次折叠的∠A
2B
2C=∠C
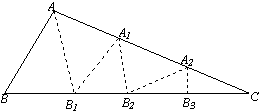
因为∠ABB
1=∠AA
1B
1,∠AA
1B
1=∠A
1B
1C+∠C,又∠A
1B
1C=∠A
1A
2B
2,∠A
1A
2B
2=∠A
2B
2C+∠C,
所以∠ABB
1=∠A
1B
1C+∠C=∠A
2B
2C+∠C+∠C=3∠C
由此可猜想若经过n次折叠∠BAC是△ABC的好角,则∠B=n∠C;
(3)因为最小角是4º是△ABC的好角,
根据好角定义,则可设另两角分别为4mº,4mnº(其中m、n都是正整数).
由题意,得4m+4mn+4=180,所以m(n+1)=44.
因为m、n都是正整数,所以m与n+1是44的整数因子,
因此有:m=1,n+1=44;m=2,n+1=22;m=4,n+1=11;m=11,n+1=4;m=22,n+1=2.
所以m=1,n=43;m=2,n=21;m=4,n=10;m=11,n=3;m=22,n=1.
所以4m=4,4mn=172;4m=8,4mn=168;4m=16,4mn=160;4m=44,4mn=132;4m=88,4mn=88.
所以该三角形的另外两个角的度数分别为:4º,172º;8º,168º;16º,160º;44º,132º;88º,88º.
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.







 寒假学与练系列答案
寒假学与练系列答案
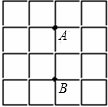
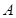 、
、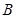 是方格纸的两个格点(即正方形的顶点),在这个
是方格纸的两个格点(即正方形的顶点),在这个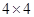 的方格纸中,找出格点
的方格纸中,找出格点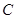 ,使
,使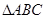 是等腰三角形,这样的点
是等腰三角形,这样的点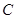 共有 个.8
共有 个.8