Question

已知二次函数y=ax²+bx+c，其中a＞0，b²-4a²c²=0，它的图象与x轴只有一个交点，交点为A，与y轴交于点B，且AB=2．
（1）求二次函数解析式；
（2）当b＜0时，过A的直线y=x+m与二次函数的图象交于点C，在线段BC上依次取D、E两点，若DE²=BD²+EC²，试确定∠DAE的度数，并简述求解过程．

Answer 1

分析：（1）由于抛物线与x轴只有一个交点，那么根的判别式△=0，联立b²-4a²c²=0，即可求出b的值及ac的关系式；将b的值代入抛物线的解析式中，即可用a、c表示出A、B的坐标，在Rt△OAB中，根据勾股定理可得到另一个关于a、c的关系式，联立上面所得的a、c的关系式，即可得到a、c的值；由此可求出该抛物线的解析式；
（2）根据（1）题所得的b＜0时抛物线的解析式，可求出A、B的坐标；根据A点的坐标即可求出直线y=x+m的解析式，进而可得到C点的坐标；若过C作CF⊥x轴于F，根据B、A、C的坐标，易证得△OAB、△BAC、△CAF都是等腰Rt△；在CF上截取CM=BD，易证得△ABD≌△ACM，可得AD=AM；已知DE²=BD²+EC²，在Rt△CEM中，根据勾股定理有：EC²+CM²=EM²，等量代换后可得到DE=ME，由此可证得△DAE≌△MAE，得∠DAE=∠EAM；而∠BAD=∠CAM，即∠BAC=∠DAM=90°，由此可得到∠DAE=45°．

解答：解法一：（1）∵y=ax²+bx+c的图象与x轴只有一个交点，
∴一元二次方程ax²+bx+c=0有两个相等的实数根，
∴△=b²-4ac=0，（1分）
又∵b²-4a²c²=0，
∴4a²c²=4ac≥0，
由AB=2，得A与B不重合，
又∵a＞0，
∴c＞0，
∴ac=1，（1）
∴b²=4解得b=±2，（2分）
∴二次函数与x轴，y轴交点坐标为A（

1

a

，0）B（0，c）或A（-

1

a

，0）B（0，c），
在Rt△ABO中，OA²+OB²=AB²，OA=

1

a

，0B=c，AB=2，
∴（

1

a

）²+c²=4，
整理得1+a²c²=4a²；（2）
把（1）代入（2），
解得a=

2

2

或a=-

2

2

（舍），
把a=

2

2

代入（1）
得c=

2

，（4分）
∴二次函数解析式为y=

2

2

x²+2x+

2

或y=

2

2

x²-2x+

2

．（5分）

（2）当b＜0时，由二次函数的解析式得A（

2

，0）B（0，

2

），（6分）
又∵直线y=x+m过点A（

2

，0），
∴m=-

2

，y=x-

2

，
由

y= 2 2 x2-2x+ 2 y=x- 2

解得，直线与二次函数图象交点C的坐标为（2

2

，

2

），（8分）
过C点作CF⊥x轴，垂足为F，可推得AB=AC，∠BAC=90°（如图所示）（9分）
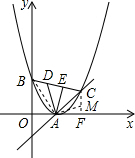
在CF上截取CM=BD，连接EM、AM，则EC²+CM²=EM²，
∵CE²+BD²=DE²，
∴EM=DE，
可证△ABD≌△ACM，
从而可证△DAE≌△MAE，（10分）
∴∠DAB=∠CAM，∠DAE=∠EAM，
∴∠DAM=∠BAC=90°，
∴∠DAE=45°．（11分）

解法二：（1）∵y=ax²+bx+c的图象与x轴只有一个交点，
∴一元二次方程ax²+bx+c=0有两个相等的实数根，
∴△=b²-4ac=0，（1分）
∵b²-4a²c²=0，
∴b=±2ac，
∴b²±2b=0，
解得b=2，b=0；b=-2，b=0，
∵b=0时，A与B两点重合
∴b=0舍去．（2分），
以下同解法一．

点评：此题是二次函数的综合题型，涉及到根的判别式、勾股定理、二次函数解析式的确定、函数图象交点坐标的求法以及全等三角形的判定和性质等重要知识，能够正确地构建与已知和所求相关的全等三角形是解答（2）题的关键．