
【题目】在矩形纸片ABCD中,AB=6,BC=8.
(1)如图①,将矩形纸片沿AN折叠,点B落在对角线AC上的点E处,求BN的长;
(2)如图②,点M为AB上一点,将△BCM沿CM翻折至△ECM,ME与AD相交于点G,CE与AD相交于点F,且AG=GE,求BM的长;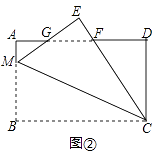
(3)如图③,将矩形纸片ABCD折叠,使顶点B落在AD边上的点E处,折痕所在直线同时经过AB、BC(包括端点),设DE=x,请直接写出x的取值范围: . 
【答案】
(1)
解:设BN=x,在Rt△ENC中,由勾股定理得:x2+42=(8﹣x),
解得:x=3,
∴BN=3
(2)
解:设BM=x,
由折叠的性质得:∠E=∠B=90°=∠A,
在△GAM和△GEF中,  ,
,
∴△GAM≌△GEF(ASA),
∴GM=GF,
∴AF=ME=BM=x,EF=AM=6﹣x,
∴DF=8﹣x,CF=8﹣(6﹣x)=x+2,
在Rt△DFC中,由勾股定理得:(x+2)2=(8﹣x)2+62,
解得:x= ![]() ,
,
∴BM= ![]()
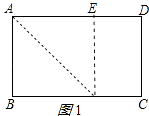
(3)解:当折痕所在直线经过点A时,如图1所示:
此时DE最小=AD﹣AB=8﹣6=2;
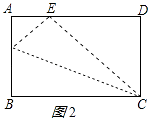
当折痕所在直线经过点C时,如图2所示:
此时DE最大,CE=CB=8,
由勾股定理得:DE= ![]() =2
=2 ![]() ;
;
∴x的取值范围是2≤x≤2 ![]() ;
;
故答案为:2≤x≤2 ![]()
【解析】(1)设BN=x,在Rt△ENC中,由勾股定理得出方程,解方程即可;(2)由ASA证明△GAM≌△GEF(ASA),得出GM=GF,AF=ME=BM=x,EF=AM=6﹣x,因此DF=8﹣x,CF=x+2,在Rt△DFC中,由勾股定理得出方程,解方程即可;(3)当折痕所在直线经过点A时,如图1所示;此时DE最小=AD﹣AB=8﹣6=2;当折痕所在直线经过点C时,如图2所示:此时DE最大,CE=CB=8,由勾股定理得:DE= ![]() =2
=2 ![]() ;∴x的取值范围是2≤x≤2
;∴x的取值范围是2≤x≤2 ![]() ;所以答案是:2≤x≤2
;所以答案是:2≤x≤2 ![]() .
.
【考点精析】通过灵活运用翻折变换(折叠问题),掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C. 
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字﹣1,﹣2,﹣3,﹣4的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(x,y)落在一次函数y=x﹣1图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F. 
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动 
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,BE=2cm,动点M、N同时出发且相遇时均停止运动,那么点M运动到第几秒钟时,与点A、E、M、N恰好能组成平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,点D、E分别是两腰AC、BC上的点,连接AE、BD相交于点O,∠1=∠2. 
(1)求证:OD=OE;
(2)求证:四边形ABED是等腰梯形;
(3)若AB=3DE,△DCE的面积为2,求四边形ABED的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com