
【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为7?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵A(﹣1,0),点B在x轴上,且AB=4,
∴﹣1﹣4=﹣5,﹣1+4=3,
∴点B的坐标为(﹣5,0)或(3,0).
(2)
解:∵C(1,4),AB=4,
∴S△ABC= ![]() AB|yC|=
AB|yC|= ![]() ×4×4=8.
×4×4=8.
(3)
解:假设存在,设点P的坐标为(0,m),
∵S△ABP= ![]() AB|yP|=
AB|yP|= ![]() ×4×|m|=7,
×4×|m|=7,
∴m=± ![]() .
.
∴在y轴上存在点P(0, ![]() )或(0,﹣
)或(0,﹣ ![]() ),使以A、B、P三点为顶点的三角形的面积为7.
),使以A、B、P三点为顶点的三角形的面积为7.
【解析】(1)由点A的坐标结合AB的长度,即可得出点B的坐标;(2)由线段AB的长度以及点C的纵坐标,利用三角形的面积公式即可求出△ABC的面积;(3)假设存在,设点P的坐标为(0,m),根据△ABP的面积为7,即可得出关于m的含绝对值符号的一元一次方程,解之即可得出点P的坐标.
【考点精析】解答此题的关键在于理解两点间的距离的相关知识,掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图. 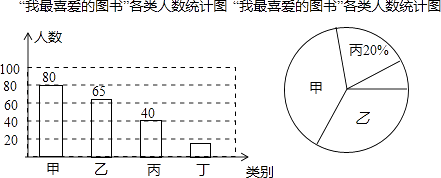
请你结合图中信息,解答下列问题(其中(1)、(2)直接填答案即可):
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生2000人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),其中a,b满足 ![]() +|2a﹣5b﹣30|=0.将点B向右平移26个单位长度得到点C,如图①所示.
+|2a﹣5b﹣30|=0.将点B向右平移26个单位长度得到点C,如图①所示.
(1)求点A,B,C的坐标;
(2)点M,N分别为线段BC,OA上的两个动点,点M从点C向左以1.5个单位长度/秒运动,同时点N从点O向点A以2个单位长度/秒运动,如图②所示,设运动时间为t秒(0<t<15).
①当CM<AN时,求t的取值范围;
②是否存在一段时间,使得S四边形MNOB>2S四边形MNAC?若存在,求出t的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式2x2+bx+c分解因式为2(x﹣3)(x+1),则b、c的值为( )
A.b=3,c=﹣1
B.b=﹣6,c=2
C.b=﹣6,c=﹣4
D.b=﹣4,c=﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把弯曲的河道改成直的,可以缩短航程,其理由是( )
A. 经过两点有且只有一条直线
B. 两点之间,线段最短
C. 两点之间,直线最短
D. 线段可以比较大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com