
����Ŀ��ij����Ͷ��һ�����͵��Ӳ�Ʒ��ÿ������ɱ�Ϊ18Ԫ�����������з��֣�ÿ��������y������������۵���x��Ԫ��֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���y����2x��100���������ۼۣ�����ɱ���
��1��д��ÿ�µ�����z����Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2�������۵���Ϊ����Ԫʱ������ÿ���ܻ��350��Ԫ���������۵���Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3��������ز��Ź涨�����ֵ��Ӳ�Ʒ�����۵��۲��ܸ���32Ԫ���������Ҫ���ÿ�²�����350��Ԫ��������ô��������ֲ�Ʒÿ�µ��������ɱ���Ҫ������Ԫ��
���𰸡���1��z����2x2��136x��1800����2�������۵���Ϊ34Ԫʱ��ÿ���ܻ����������������Ϊ512��Ԫ����3��ÿ���������ɱ�Ϊ648��Ԫ
����������1������ÿ�µ�����z=��x-18��y���ٰ�y=-2x+100���뼴�����z��x֮��ĺ�������ʽ��
��2����z=350����z=-2x2+136x-1800����������̼��ɣ���z�T-2x2+136x-1800�䷽����z=-2��x-34��2+512��������������۵���Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3����ϣ�2��������z=-2x2+136x-1800��ͼ�������25��x��43ʱz��350���ٸ�����32Ԫ���ó�25��x��32��������һ�κ���y=-2x+100��y��x���������С�����ɵó���x=32ʱ��ÿ������ɱ���ͣ���ͳɱ���18����-2��32+100��
�⣺��1��z=��x-18��y=��x-18����-2x+100��
=-2x2+136x-1800��
��z��x֮��ĺ�������ʽΪz=-2x2+136x-1800��
��2����z=350����350=-2x2+136x-1800��
��������̵�x1=25��x2=43
���ԣ����۵��۶�Ϊ25Ԫ��43Ԫ��
��z�T-2x2+136x-1800�䷽����z=-2��x-34��2+512��
�𣻵����۵���Ϊ34Ԫʱ��ÿ���ܻ������������������512��Ԫ��
��3����ϣ�2��������z=-2x2+136x-1800��ͼ����ͼ��ʾ����֪��

��25��x��43ʱz��350��
������32Ԫ����25��x��32��
����һ�κ��������ʣ���y=-2x+100��y��x���������С��
��x���ȡ32��
�൱x=32ʱ��ÿ������ɱ���ͣ���ͳɱ���18����-2��32+100��=648����Ԫ������ÿ���������ɱ�Ϊ648��Ԫ��
���㾦�����⿼����Ƕ��κ�����ʵ�������е�Ӧ�ã��ؼ��Ǹ�������������κ����Ľ���ʽ���ۺ����ö��κ�����һ�κ��������ʽ��ʵ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��CΪ�����ϵ����㣬����A��Bͬʱ��ԭ�����������Aÿ���˶�x����λ������Bÿ���˶�y����λ���Ҷ���A�˶�����λ�ö�Ӧ������Ϊa������B�˶�����λ�ö�Ӧ������Ϊb������C��Ӧ����Ϊ8��
��1����2���a��b����|a+8|+��b��2��2=0����x= �� y= �� �����������ϱ��A��B�����λ�ã�
��2��������A��B�ڣ�1���˶����λ���ϱ���ԭ�����ٶȣ���ͬʱ���������˶�z���ʹ��|a|=|b|��ʹ��z= ��
��3��������A��B�ڣ�1���˶����λ���϶���ÿ��2����λ���������˶������˶�t�룬��A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC����A���B֮��ľ���ΪAB����AC+BC=1.5AB����t= �� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����������ε����߳��ֱ�Ϊ5���ס�9���ף�����������ε��ܳ�Ϊ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��������֪ʶ��С�վͱ���ѧ������֪ʶ���˽�̶Ƚ�����һ�ε���ͳ�ƣ�A����Ϥ��B���˽�϶࣬C��һ���˽⣮ͼ1��ͼ2�����ɼ����ݺ��Ƶ�������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺ 
��1����ð�ж�����ѧ����
��2��������ͼ�У�����ʾ��һ���˽⡱�IJ��ֲ���������
��3��������ͳ��ͼ�У���������˽�϶ࡱ��������Ӧ��Բ�ĽǵĶ�����
��4�����ȫ�꼶��1000��ͬѧ���������ȫ�꼶����֪ʶ���˽�϶ࡱ��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACB�͡�DCE��Ϊ���������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��1����ͼ1������CAB=��CBA=��CDE=��CED=50��
����֤��AD=BE��
�����AEB�Ķ�����
��2����ͼ2������ACB=��DCE=120�㣬CMΪ��DCE��DE���ϵĸߣ�BNΪ��ABE��AE���ϵĸߣ���֤����AE=![]() CM+
CM+![]() BN��
BN��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪A��0��a����B��b��0��������a��b����|a��2|+��b��3��2=0��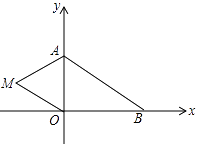
��1��a= �� b=��
��2������ڵڶ���������һ��M��m��1�������ú�m��ʽ�ӱ�ʾ�ı���ABOM�������
��3���ڣ�2�������£���m=�� ![]() ʱ����������ĸ����������N�������꣩��ʹ�á�ABN��������ı���ABOM�������ȣ���ֱ��д���𰸣�
ʱ����������ĸ����������N�������꣩��ʹ�á�ABN��������ı���ABOM�������ȣ���ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com