
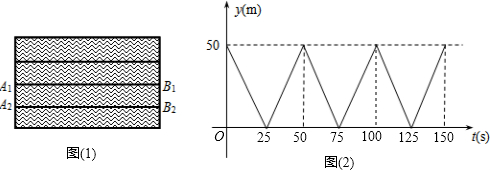
分析 (1)由函数图象可以直接得出赛道的长度为50米,由路程÷时间=速度就可以求出甲的速度;设经过x秒时,甲、乙两人第二次相遇,根据甲游过的路程+乙游过的路程,建立方程求出其解即可;
(2)由速度与时间的关系就可以求出结论.
解答 解:(1)由图象,得赛道的长度是:50米,
甲的速度是:50÷25=2m/s.
故答案为:50,2;
设经过x秒时,甲、乙两人第一次相遇,由题意,2x+1.5x=50,
∴x=$\frac{100}{7}$,
设经过x秒时,甲、乙两人第二次相遇,由题意,得
2x+1.5x=150,
解得:x=$\frac{300}{7}$;
故答案为:50,2,$\frac{100}{7}$,$\frac{300}{7}$;
(2)设经过x s后两人第三次相遇,则(1.5+2)x=250 得x=$\frac{500}{7}$,
∴第三次相遇时,两人距池边B1B 2 有150-$\frac{500}{7}$×2=$\frac{50}{7}$ m.
点评 本题考查了行程问题的数量关系速度=路程÷时间的运用,相遇问题的数量关系的运用,解答时认真分析函数图象的意义是关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
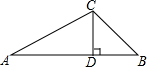 南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)
南沙群岛是我国股友领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至A处时,该岛位于正东方向的B处,为了防止某国海巡警干扰,就请求我国C处的渔监船前往B处护航,测得C与AB的距离CD为20海里,已知A位于C处的南偏西60°方向上,B位于C的南偏东45°的方向上,求A、B之间的距离.($\sqrt{3}$≈1.7,结果精确到1海里)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com