
已知:如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,可以说明:△ACN≌△MCB,从而得到结论:AN=BM.现要求:
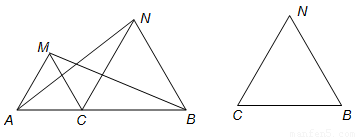
(1)将△ACM绕C点按逆时针方向旋转180°,使A点落在CB上.请对照原题图在下图中画出符合要求的图形(不写作法,保留作图痕迹).
(2)在(1)所得到的图形中,结论“AN=BM”是否还成立?若成立,请给予证明;若不成立,请说明理由.
(3)在(1)所得到的图形中,设MA的延长线与BN相交于D点,请你判断△ABD与四边形MDNC的形状,并说明你的结论的正确性.
(1)作图见试题解析;(2)成立.证明见试题解析;(3)△ABD是等边三角形,四边形MDNC是平行四边形.理由见试题解析.
【解析】
试题分析:(1)可以C为圆心以CA为半径,画弧交BC于A,然后分别以C,A为圆心,以CA长为半径,画弧在BC下方交于M连接CM,AM,三角形ACM就是所求的三角形;
(2)还成立,可通过证明三角形ACN和BCM来实现,这两个三角形中,CN=BC,CA=CM,这两组对应边的夹角都等于60°,因此两三角形全等,即可得出AN=BM;
(3)MA的延长线与BN相交于D点,那么对顶角DAB和CAM都应该是60°,∠NBC也是60°,那么三角形ABD是等边三角形.∠DAB=∠NCB=60°,因此MD∥CN,∠MCB=∠NBC=60°,因此CM∥NB,因此四边形CMDN就是个平行四边形.
试题解析:(1)如下图.

(2)结论“AN=BM”还成立.证明:∵CN=CB,∠ACN=∠MCB=60°,CA=CM,∴△ACN≌△MCB(SAS),∴AN=BM.
(3)△ABD是等边三角形,四边形MDNC是平行四边形.
证明:∵∠DAB=∠MAC=60°,∠DBA=60°,∴∠ADB=60°.∴△ABD是等边三角形,∵∠ADB=∠AMC=60°,∴ND∥CM,∵∠ADB=∠BNC=60°,∴MD∥CN,∴四边形MDNC是平行四边形.
考点:1.尺规作图;2.全等三角形的判定;3.等边三角形的判定与性质;4.平行四边形的判定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 26、已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
26、已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
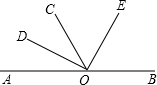 已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com