
【题目】如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD. 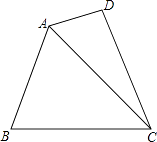
(1)求∠ADC的度数;
(2)若AB=10cm,CD=12cm,求四边形ABCD的面积.
【答案】
(1)解:作CE⊥AB交AB于点E,则∠AEC=90°,
∵AC=BC,
∴CE是AB的垂直平分线,
∴AE=BE= ![]() AB,
AB,
∵AB=2AD,
∴AE=AD= ![]() AB,
AB,
∵∠AC平分∠BAD,
∴∠EAC=∠DAC,
在△ADC和△AEC中,
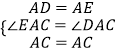 ,
,
∴△ADC≌△AEC,
∴∠ADC=∠AEC=90°
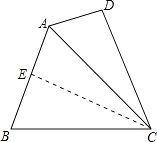
(2)解:∵CE是AB的垂直平分线,
∴S△ACD=S△AEC,
∵AB=2AD,CD=CE,
∴S△ACB=2S△ADC,
∴四边形ABCD的面积=3S△ADC=3× ![]() ×5×12=90cm2.
×5×12=90cm2.
【解析】(1)作CE⊥AB交AB于点E,则∠AEC=90°,利用已知条件和全等三角形的判定方法可证明△ADC≌△AEC,利用全等三角形的性质即可得到∠ADC=∠AEC=90°;(2)由(1)可知S△ACD=S△AEC , 再根据高相等的两个三角形面积比等于底之比可得S△ACB=2S△ADC , 进而四边形ABCD的面积=3S△ADC , 问题得解.


科目:初中数学 来源: 题型:
【题目】下列事件中是不可能事件的是( )
A.任意画一个四边形,它的内角和是360°
B.若a=b,则a2=b2
C.掷一枚质地均匀的硬币,落地时正面朝上
D.一只袋子里共装有3个小球,它们的标号分别为1,2,3,从中摸出一个小球,标号为5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个说法中,正确的是( )
A. 相等的角是对顶角
B. 平移不改变图形的形状和大小,但改变直线的方向
C. 两条直线被第三条直线所截,内错角相等
D. 两直线相交形成的四个角相等,则这两条直线互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句错误的是( )
A.连接两点的线段的长度叫做两点间的距离
B.两条直线平行,同旁内角互补
C.若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角
D.平移变换中,各组对应点连成两线段平行且相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com