
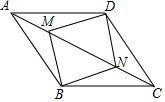
 如图,点M、N在?ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.
如图,点M、N在?ABCD的对角线AC上,且AM=CN,求证:四边形BMDN是平行四边形.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
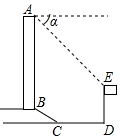 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3).
如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
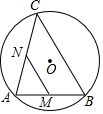 如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是$\frac{5\sqrt{2}}{2}$.
如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是$\frac{5\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com