
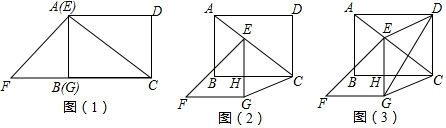
���� ��1���ȸ��ݹ��ɶ����ó�AC�����жϳ���ABOΪ����ֱ�������Σ��������AE�����ɣ�
��2������������������ۼ��㣬���õ��������εı���Ƚ���������⼴�ɵó����ۣ�
��3�����жϳ��ı���CDEG�����Σ��ٹ���ֱ�������������ADE�ı�AD�ϵĸߣ��������ɵó����ۣ�
��� �⣺��1��������ã�AB=6��BC=8 EG=EF=AB=CD=6��
��Rt��ABC�У����ݹ��ɶ������ã�AC=10��
��EFͨ��B��ʱ����EG��BC����ΪO��
������֪����BAF=��BAC=45�㣬
���FAC=90�㣬
���ABOΪ����ֱ�������Σ�
��Rt��ABO��AB=6��
��AE=$\frac{\sqrt{2}}{2}$AB=3$\sqrt{2}$��
��t=AE��5=3$\sqrt{2}$��5=$\frac{3\sqrt{2}}{5}$��
��2����������CEG����������
��ٵ�CE=EGʱ����CE=EG=6��
��AE=AC-CE=4��
��t=$\frac{4}{5}$��
�ڵ�EG=CGʱ���ߡ�AEF=90�㣬��FEG=45�㣬
���CEG=45�㣬
���ECG=45�㣬
���EGC=90�㣬
��BC��EG��
���G��BC�ϣ�
������G�͵�B�غϣ�
��ʱ��CG=8��EG=6��
��EG��CG�����������������
�۵�CE=CGʱ�����CEG=��CGE��
�ߡ�CEG=45�㣬
���ECG=90�㣬
��Rt��CEG�У���CEG=��CGE=45�㣬EG=6��
��CE=$\frac{\sqrt{2}}{2}$EG=3$\sqrt{2}$��
��AE=AC-CE=10-3$\sqrt{2}$��
��t=$\frac{10-3\sqrt{2}}{5}$��
��3����ͼ3�� ��EG��CD��EG=CD��
��EG��CD��EG=CD��
���ı���CDEG��ƽ���ı��Σ�
��DG��AC��
��ƽ���ı���CDEG�����Σ�
��CD=DE=EG=6
�ӳ�EG��AD����P�㣬EM��EG��AB����M�㣬
���ı���APEM�Ǿ��Σ�
��PE=AM��AP=EM��
��EM��AB��BC��AB��
��EM��BC��
��$\frac{AM}{AB}=\frac{EM}{BC}$��
��$\frac{AM}{6}=\frac{EM}{8}$��
��$\frac{AM}{EM}=\frac{3}{4}$��
��AM=$\frac{3}{4}$EM��
��AP=$\frac{4}{3}$PE��
��DP=AD-AP=8-$\frac{4}{3}$PE��
��Rt��DPE�У����ݹ��ɶ����ã�DP2+PE2=DE2��
�ࣨ8-$\frac{4}{3}$PE��2+��$\frac{4}{3}$PE��2=36��
��PE=$\frac{36+3\sqrt{130}}{4}$���ᣩ��PE=$\frac{36-3\sqrt{130}}{4}$��
��S�ı���CDEG=2��S��ACD-S��ADE��=2��$\frac{1}{2}$��6��8-$\frac{1}{2}$��8��$\frac{36-3\sqrt{130}}{4}$��=6$\sqrt{130}$-24��
���� �������ı����ۺ��⣬��Ҫ������ƽ���ı��ε��ж������ʣ����ε����ʺ��ж������ε��ж������ʣ����������ε��жϺ����ʣ����ɶ������Ȿ��Ĺؼ��ǹ���ֱ�������Σ���һ���ۺ��ԱȽ�ǿ�ۺ��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
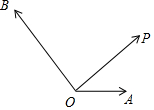 ��ͼ����֪����$\overrightarrow{OA}$��$\overrightarrow{OB}$��$\overrightarrow{OP}$��
��ͼ����֪����$\overrightarrow{OA}$��$\overrightarrow{OB}$��$\overrightarrow{OP}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
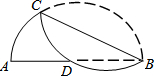 ��ͼ����BC����BC�۵���ֱ��AB�ڵ�D����AD=5��DB=7����BC�ij���$\sqrt{114}$��
��ͼ����BC����BC�۵���ֱ��AB�ڵ�D����AD=5��DB=7����BC�ij���$\sqrt{114}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��Ȥ�����⣬̫�ˣ�
��Ȥ�����⣬̫�ˣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
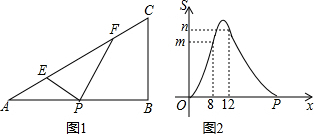
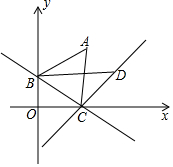 ��ͼ��ֱ��y=-$\frac{\sqrt{3}}{3}$x+2��x�ύ�ڵ�C����y�ύ�ڵ�B����A�ڵ�һ�����ڣ���ABC���������Σ���D��ֱ��y=x-2$\sqrt{3}$�ϵ�һ������һ�㣬��DBC�͡�ABC�����ȣ����D�������ǣ�6��6-2$\sqrt{3}$����
��ͼ��ֱ��y=-$\frac{\sqrt{3}}{3}$x+2��x�ύ�ڵ�C����y�ύ�ڵ�B����A�ڵ�һ�����ڣ���ABC���������Σ���D��ֱ��y=x-2$\sqrt{3}$�ϵ�һ������һ�㣬��DBC�͡�ABC�����ȣ����D�������ǣ�6��6-2$\sqrt{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com