
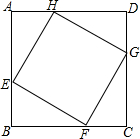
 如图,正方形ABCD的长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH,则四边形EFGH面积的最小值是32cm2.
如图,正方形ABCD的长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH,则四边形EFGH面积的最小值是32cm2. 分析 先证出四边形EFGH是菱形,再证出∠HEF=90°,即可得到四边形EFGH是正方形;再设四边形EFGH面积为S,BE=xcm,则BF=(8-x)cm,由勾股定理得出S=x2+(8-x)2=2(x-4)2+32,S是x的二次函数,容易得出四边形EFGH面积的最小值.
解答 解:
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG,
在△AEH、△BFE、△CGF和△DHG中,
$\left\{\begin{array}{l}{AE=BF=CG=DH}\\{∠A=∠B=∠C=∠D}\\{AH=BE=CF=DG}\end{array}\right.$,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形;
设四边形EFGH面积为S,设BE=xcm,则BF=(8-x)cm,
根据勾股定理得:EF2=BE2+BF2=x2+(8-x)2,
∴S=x2+(8-x)2=2(x-4)2+32,
∵2>0,
∴S有最小值,
当x=4时,S的最小值=32,
∴四边形EFGH面积的最小值为32cm2,
故答案为:32.
点评 本题考查了正方形的性质与判定、菱形的判定、全等三角形的判定与性质、勾股定理、三角函数、二次函数的最值等知识;本题综合性强,有一定难度,需要证明三角形全等和运用二次函数才能得出结果.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 向下平移了2个单位 | B. | 向上平移了2个单位 | ||
| C. | 向左平移了2个单位 | D. | 向右平移了2个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 梯形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com