
【题目】如图,直线AB交CD于点O,OE平分∠BOC,OF平分∠BOD,∠AOC=3∠COE,则∠AOF等于___________.

科目:初中数学 来源: 题型:
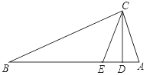
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
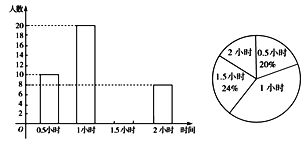
【题目】某中学为了解学生每天参加户外活动的情况,对部分学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)这次抽样调查,一共抽查了 名学生;
(2)补全频数分布直方图;
(3)若该中学共有1500名学生,请估计该校每天参加户外活动的时间为1小时的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,给出如下定义:若存在点
,给出如下定义:若存在点![]() (
(![]() 为正数),称点
为正数),称点![]() 为点
为点![]() 的等距点.例如:如图,对于点
的等距点.例如:如图,对于点![]() ,存在点
,存在点![]() ,点
,点![]() ,则点
,则点![]() 分别为点
分别为点![]() 的等距点.
的等距点.
(1)若点![]() 的坐标是
的坐标是![]() ,写出当
,写出当![]() 时,点
时,点![]() 在第一象限的等距点坐标;
在第一象限的等距点坐标;
(2)若点![]() 的等距点
的等距点![]() 的坐标是
的坐标是![]() ,求当点
,求当点![]() 的横、纵坐标相同时的坐标;
的横、纵坐标相同时的坐标;
(3)是否存在适当的![]() 值,当将某个点
值,当将某个点![]() 的所有等距点用线段依次连接起来所得到的图形周长不大于
的所有等距点用线段依次连接起来所得到的图形周长不大于![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】主持人站在舞台的黄金分割点处最自然得体,如果舞台AB长为20米,一个主持人现站在舞台AB的黄金分割点点C处,则下列结论一定正确的是( )
①AB:AC=AC:BC;
②AC≈6.18米;
③AC=10(![]() )米;
)米;
④BC=10(3![]() )米或10(
)米或10(![]() 1)米.
1)米.
A. ①②③④ B. ①②③ C. ①③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连接四边形ABCD四边中点得到新的四边形为菱形,那么原四边形ABCD为( )
A. 矩形
B. 菱形
C. 对角线相等的四边形
D. 对角线垂直的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
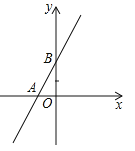
【题目】如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,求P点的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室内的饮水机接通电源进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(分钟)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为30℃时,接通电源后,水温y(℃)和时间x(分钟)的关系如图.
(1)a= ;
(2)直接写出图中y关于x的函数关系式;
(3)饮水机有多少时间能使水温保持在70℃及以上?
(4)若饮水机早上已加满水,开机温度是20℃,为了使8:40下课时水温达到70℃及以上,并节约能源,直接写出当它上午什么时间接通电源比较合适?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com