
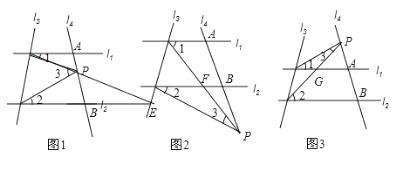
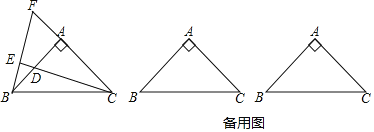
����Ŀ����ֱ֪��l1��l2����l4��l1��l2�ֱ���A��B���㣬��PΪ�߶�AB�ϣ���һ�����㣨��ͼ1��

��1��д����1����2����3��֮��Ĺ�ϵ��˵�����ɣ�
��2�������PΪ�߶�AB�ϣ��Ķ���ʱ������1����2����3֮��Ĺ�ϵ�Ƿ����仯��������˵���ɣ�
��3�������P��A��B��������˶�ʱ�� ����P�͵�A����B���غϣ�
����ͼ2������P������AB���˶�ʱ����1����2����3֮���ϵ��˵�����ɣ�
����ͼ3������P������BA���˶�ʱ����1����2����3֮���ϵ����˵���ɣ�
���𰸡���1����3=��1+��2 ���ɣ���������2�����䣨3���١�1=��2+��3 ���ɣ�������
�ڡ�2=��1+��3
��������
��1����3=��1+��2 ���ɣ�
�ӳ�DP��ֱ��l2��E����ͼ1
��ֱ��l1��l2
���1=��DCE
�ߡ�3=��DEC+��2
���3=��1+��2
��2���������仯����3=��1+��2
���ɣ�
��ֱ��l1��l2
���1=��DCE
���3=��DEC+��2=��1+��2
��3��������P������AB���˶�ʱ����ͼ2
��ֱ��l1��l2
���1=��PFB
�ߡ�PFB=��2+��3
���1=��2+��3
����ͼ3������P������BA���˶�ʱ��
��ֱ��l1��l2
���PGA=��2
�ߡ�PGA=��1+��3
���2=��1+��3



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
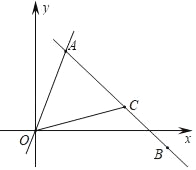
����Ŀ����ͼ��ֱ��OA��ֱ��BC�ཻ�ڵ�A���ҵ�B������Ϊ��5����1������C������Ϊ��3��1����ֱ��OA�Ľ���ʽΪy��3x
��1����ֱ��BC�Ľ���ʽ��
��2�����A�����ꣻ
��3������OAC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������A��B�����������֪A������ĵ��۱�B������ĵ��۶�30Ԫ������900Ԫ����A���������������600Ԫ����B�������������ȣ�
��1����A��B��������ĵ��ۣ�
��2��������Ҫ������������A��B���������200����������������������ܷ��ò�����14700Ԫ��������A��������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�ζ�������ͬ��С�ġ���һ��������ɵģ����еڣ�����ͼ����һ����3�������ڢڸ�ͼ����һ����8�������ڢ۸�ͼ����һ����14�������������˹���������ȥ���ڢ��ͼ���еġ�����Ϊ( )
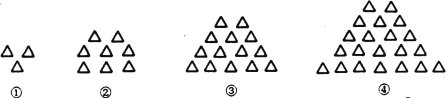
A. 54B. 61C. 71D. 77
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
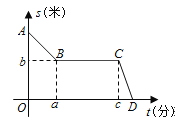
����Ŀ������ʦΪ��������һֱ��ֲ������°ࡣ��֪ѧУ������ʦ����·��Ϊ2000�ף�һ�죬����ʦ�°����45��/�ֵ��ٶȴ�ѧУ�����ߣ��ߵ���ѧУ900��ʱ����������һ�����ѣ�ͣ��������20���ӣ�֮����110��/�ֵ��ٶ����˼ң�����ʦ�ؼҹ����У���ҵ�·��S���ף�������ʱ��t���֣�֮��Ĺ�ϵ��ͼ��ʾ��
��1����a��ֵ��
��2��b= ��c= .
��3��������ʦ��ѧУ���ҵ�ƽ���ٶȡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������֤����
��֪����ͼ����AED=��C����DEF=��B����֤����1=��2��

֤�����ߡ�AED=��C����֪����
�� �� �� ����
���B+��BDE=180���� ����
�ߡ�DEF=��B����֪����
���DEF+��BDE=180����������������
�� �� �� ����
�� ��1=��2�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����BAC=90�㣬��D��ֱ��AB�ϵ�һ���㣨����A��B�غϣ���BE��CD��E����ֱ��AC��F��
(1)��D�ڱ�AB��ʱ��֤����AB=FA+BD��
(2)��D��AB���ӳ������ӳ�����ʱ��(1)�еĽ����Ƿ�����������������뻭��ͼ�β�ֱ��д����ȷ���ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ��ķ��������з��̻��飺
��1��5-x=18
��2��4x+3=2(x-1)+1
��3��![]()
��4��![]()
��5��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ȴ�����ˮ��֮һ������Ӫ����Ϊ�ḻ�����е����ʡ����ࡢ����ά���ء���ʳ��ά��֬����Ҷ�ᣬ������Ϳ����ʣ���ǿ�����塢��������֮��Ч��������ζŨ�ҡ���֮�������㣬��֮��Թ�����ϲ����������Ҳϲ�������ɣ�����ǧ�㣬���������������ֵ������ӹ���Ʒ��ijУ��ѧ��ȤС��Ϊ���˽ⱾУѧ��ϲ������������������ȡ��200��ѧ�����ʾ����飬����ͳ�ƺ�����������в�������ͳ��ͼ����ע��ÿһλͬѧ���κ�һ�ַ���ͳ����ֻ��һ��ѡ��

�����ͳ��ͼ����������⣺
��1������ͳ��ͼ�У�����ϲ��������Ӧ��Բ�ĽǶ���Ϊ______�ȣ�ϲ������ǧ�������Ϊ______�ˣ��벹ȫ����ͳ��ͼ��
��2������Уѧ������Ϊ8000�ˣ���������������������Ƹ�Уѧ������������ɺ������ֵ�����֮�ͣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com