
【题目】下列说法正确的是( )
A.“买一张电影票,座位号为偶数”是必然事件
B.若甲、乙两组数据的方差分别为s ![]() =0.3、s
=0.3、s ![]() =0.1,则甲组数据比乙组数据稳定
=0.1,则甲组数据比乙组数据稳定
C.一组数据2,4,5,5,3,6的众数是5
D.若某抽奖活动的中奖率为 ![]() ,则参加6次抽奖一定有1次能中奖
,则参加6次抽奖一定有1次能中奖
【答案】C
【解析】解:A、“买一张电影票,座位号为偶数”是随机事件,故A选项错误;
B、若甲、乙两组数据的方差分别为s ![]() =0.3、s
=0.3、s ![]() =0.1,则乙组数据比甲组数据稳定,故B错误;
=0.1,则乙组数据比甲组数据稳定,故B错误;
C、5出现的次数最多,故这组数据的众数为5,故C正确;
D、若某抽奖活动的中奖率为 ![]() ,则参加6次抽奖可能有1次的中奖机会,故D错误;
,则参加6次抽奖可能有1次的中奖机会,故D错误;
故选C.
【考点精析】本题主要考查了随机事件和概率的意义的相关知识点,需要掌握在条件S下,一定会发生的事件,叫相对于条件S的必然事件;在条件S下,一定不会发生的事件,叫相对于条件S的不可能事件;在条件S下可能发生也可能不发生的事件,叫相对于S的随机事件;任何事件的概率是0~1之间的一个确定的数,它度量该事情发生的可能性.小概率事件很少发生,而大概率事件则经常发生.知道随机事件的概率有利于我们作出正确的决策才能正确解答此题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2,CD=4,点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.当B点运动到线段CD上时,P是线段AB上一点,且有关系式![]() =3成立,则线段PD的长为______________.
=3成立,则线段PD的长为______________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多肉植物是指植物营养器官肥大的植物,又称肉质植物或多肉花卉,由于体积小、外形萌、色彩斑斓,茶几阳台摆放方便,近年来越来越受到广大养花爱好者的喜爱.多肉植物则被亲切地称为“肉肉”、“多肉君”.大学毕业生陈江河发现这个商机后,第一次果断购进甲乙两种多肉植物共500株.甲种多肉植物每株成本5元,售价10元;乙种多肉植物每株成本8元,售价10元.
(1)由于启动资金有限,第一次购进多肉植物的金额不得超过3400元,则甲种多肉植物至少购进多少株?
(2)多肉植物一经上市,十分抢手,陈江河决定第二次购进甲乙两种多肉植物,它们的进价不变.甲种多肉植物进货量在(1)的最少进货量的基础上增加了![]() ,售价也提高了
,售价也提高了![]() ;乙种多肉植物的售价和进货量不变,但是由于乙种多肉植物的耐热性不强,导致销售完之前它的成活率为
;乙种多肉植物的售价和进货量不变,但是由于乙种多肉植物的耐热性不强,导致销售完之前它的成活率为![]() .结果第二次共获利2700元.求m的值.
.结果第二次共获利2700元.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
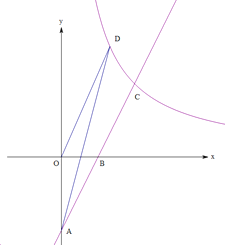
【题目】如图,在平面直角坐标系中,直线![]() 与坐标轴交于
与坐标轴交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]() 在第一象限内的图像交于点
在第一象限内的图像交于点![]() ,反比例函数图像上有一点
,反比例函数图像上有一点![]() ,连接
,连接![]() 和
和![]() ,已知:
,已知: ![]() .
.
(1)求一次函数和反比例函数的解析式.
(2)求△AOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算中,能用平方差公式计算的是( )
A. (﹣a+b)(a﹣b)B. (a﹣b)(﹣b+a)
C. (3a﹣b)(3b+a)D. (b+2a)(2a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
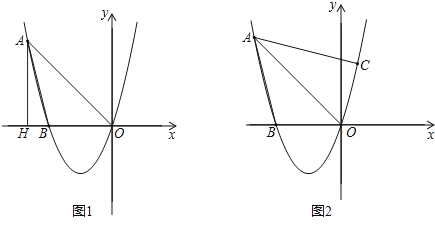
【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片ABCD按如图所示的方式折叠,AE,EF为折痕,∠BAE=30°,AB= ![]() ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( ) 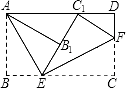
A.![]()
B.2
C.3
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市开展“阳光”活动中,为解中学生活动开展情况,随机抽查全市八年级部分同学1分钟,将抽查结果进行,并绘制两个不完整图.请根据图中提供信息,解答问题:
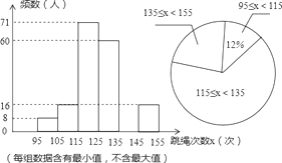
(1)本次共抽查多少名学生?
(2)请补全直方图空缺部分,直接写扇形图中范围135≤x<155所在扇形圆心角度数.
(3)若本次抽查中,在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生成绩为优秀?
(4)请你根据以上信息,对我市开展学生活动谈谈自己看法或建议
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com