
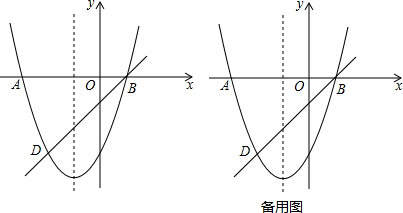
���� ��1����A��D��������������κ�������ʽ�ɵö��κ�������ʽ��b��c��ֵ��
��2���ö��κ�����y����0�����������x��Ľ���B����B��D�������һ�κ�������ʽ�ɵ�ֱ��BD�Ľ���ʽ���õ���a��ʾ��EF�Ľ���ʽ�������κ�������ʽ��ɷ����飬�õ���y��һԪ���η��̣���������y=-3��ú��ʵ�a��ֵ���ɣ�
��3�����������ߵĽ���ʽ��ֱ�ߵĽ���ʽ�����P��M�����꣬���������г�PM=|m2+2m-3-��m-1��|=|m2+m-2|=|��m+$\frac{1}{2}$��2-$\frac{9}{4}$|��������ã�
��� �⣺��1����A��-3��0����D��-2��-3�����������y=x2+bx+c�ã�
$\left\{\begin{array}{l}{9-3b+c=0}\\{4-2b+c=-3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=2}\\{c=-3}\end{array}\right.$��
��������ߵĽ���ʽΪ��y=x2+2x-3��
��2����ͼ1���ɣ�1��֪�������ߵĽ���ʽΪ��y=x2+2x-3��
��y=0����x2+2x-3=0��
�ã�x1=-3��x2=1��
��B�������ǣ�1��0����
��ֱ��BD�Ľ���ʽΪy=kx+b��k��0������
$\left\{\begin{array}{l}{k+b=0}\\{-2k+b=-3}\end{array}\right.$��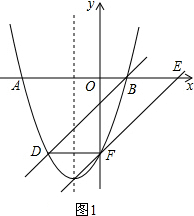
��ã�$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$��
��ֱ��BD�Ľ���ʽΪy=x-1��
�֡�EF��BD��
��ֱ��EF�Ľ���ʽΪ��y=x-a��
���ı���BDFE��ƽ���ı��Σ�
��DF��x�ᣬ
��D��F�������������ȣ�����F��������Ϊ-3��
��$\left\{\begin{array}{l}{y={x}^{2}+2x-3}\\{y=x-a}\end{array}\right.$����
��y=x-a�ã�x=y+a�����뷽��y=x2+2x-3�ã�
y2+��2a+1��y+a2+2a-3=0��
��ã�y=$\frac{-��2a+1����\sqrt{13-4a}}{2}$��
��$\frac{-��2a+1����\sqrt{13-4a}}{2}$=-3��
��ã�a1=1��a2=3��
��a=1ʱ��E������꣨1��0��������B���غϣ���ȥ��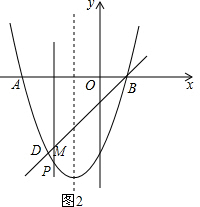
�൱a=3ʱ��E������꣨3��0�����������⣮
�����ʵ��a=3��ʹ�ı���BDFE��ƽ���ı��Σ�
��3����M��m��m-1������P��m��m2+2m-3����
��PM=|m2+2m-3-��m-1��|=|m2+m-2|=|��m+$\frac{1}{2}$��2-$\frac{9}{4}$|��
�൱m=-$\frac{1}{2}$ʱ��PM�����ֵ�����ֵΪ$\frac{9}{4}$��
��ʱP��-$\frac{1}{2}$��$\frac{3}{2}$����
���P����Ϊ��-$\frac{1}{2}$��$\frac{3}{2}$��ʱ���߶�PE���������ֵ�����ֵ��$\frac{9}{4}$��
���� �����ۺϿ����˶��κ����ۺ��⣮�����漰���˴���ϵ������һ�κ��������κ�������ʽ����ԳƵ����ʣ����κ�����ֵ�����Լ�ƽ���ı��ε��ж������ʣ�ƽ��ֱ������ϵ�У���ֱ��ƽ�У�һ����ϵ����ֵ��ȣ����������ڵ�ֱ��ƽ�У������������������ȣ�


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 0 | C�� | -1 | D�� | -$\sqrt{15}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com