
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
科目:初中数学 来源: 题型:
【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。
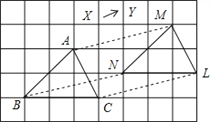
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,E是CD上的一点连接AE、BE,如图给出四个条件:①AE平分∠BAD,②BE平分∠ABC,③AE⊥EB,④AB=AD+BC,请你以其中三个作为命题的条件,写出一个能推出AD∥BC的正确命题,并加以证明.
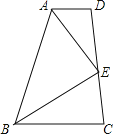
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员把全班45名同学的体育锻炼时间,并绘制了如图所示的折线统计图,则全班45名同学一周的体育锻炼总时间的众数和中位数分别是( ) 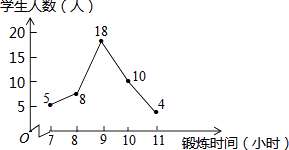
A.9,9
B.9,10
C.18,9
D.18,18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com