

���� ��1���ɵ��������ε����ʵõ������εĸߣ��ٸ������������Ƶõ�����ʽ������εĸߣ��������ε������ʽ���㼴�ɣ�
��2��������������ۣ��������������ƣ��������Ӧͼ�εĵߣ�������Ӧͼ�ε������ʽ���ɵõ������
��3������ADE�Ƶ�O��˳ʱ����ת15�㣬��˳ʱ����ת60�㣬����ʱ����ת30�㣬����ʱ����ת75��ʱ����CPQΪ���������Σ�
��� �⣺��1���ߡ�ABCΪ�߳�Ϊ6�ĵȱ������Σ�
��AH=3$\sqrt{3}$��
��DE��BC��
���ADE�ס�ABC��
��$\frac{DE}{BC}=\frac{AD}{AB}$=$\frac{AO}{AH}$��
��AD=2BD��
��$\frac{DE}{BC}=\frac{AD}{AB}$=$\frac{AO}{AH}$=$\frac{2}{3}$��
��$DE=4��AO=2\sqrt{3}$��
��OH=$\sqrt{3}$��
S����BCED=$\frac{1}{2}$��4+6��$•\sqrt{3}$=5$\sqrt{3}$��
��2���ٵ�0��t��$\sqrt{3}$ʱ����ͼ1��
������ã�D��E��=DE=4��A��O��=2$\sqrt{3}$��AA��=t��
��PQ��D��E�䣬
���A��PQ�ס�A��D��E�䣬
��$\frac{PQ}{D��E��}=\frac{A��O}{A��O��}$��
��PQ=$\frac{4\sqrt{3}-2t}{\sqrt{3}}$��
��S=$\frac{1}{2}$��$\frac{4\sqrt{3}-2t}{\sqrt{3}}$+4��•t=-${\frac{\sqrt{3}}{3}t}^{2}$+4t����0��t��$\sqrt{3}$����
�ڵ�$\sqrt{3}$��t$��2\sqrt{3}$ʱ����ͼ2��
�ɢ�֪��MN=$\frac{4\sqrt{3}-2t}{\sqrt{3}}$��
�ɡ�A��D��E��ס�ABC��
��$\frac{PQ}{BC}$=$\frac{A��H}{AH}$��
��PQ=$\frac{6\sqrt{3}-2t}{\sqrt{3}}$��
��S=$\frac{1}{2}$��$\frac{4\sqrt{3}-2t}{\sqrt{3}}$+$\frac{6\sqrt{3}-2t}{\sqrt{3}}$��$•\sqrt{3}$=-2t+5$\sqrt{3}$����$\sqrt{3}��t��2\sqrt{3}$����
�۵�2$\sqrt{3}$��t��3$\sqrt{3}$ʱ����ͼ3��
�ɢ�֪PQ=$\frac{6\sqrt{3}-2t}{\sqrt{3}}$��A��H=3$\sqrt{3}$-t��
��S=$\frac{1}{2}$•$\frac{6\sqrt{3}-2t}{\sqrt{3}}$•��3$\sqrt{3}$-t��=-$\frac{\sqrt{3}}{3}$t2-6t+9$\sqrt{3}$����2$\sqrt{3}$��t$��3\sqrt{3}$����
��S=$\left\{\begin{array}{l}{-{\frac{\sqrt{3}t}{3}}^{2}+4t��0��t��\sqrt{3}��}\\{-2t+5\sqrt{3}��\sqrt{3}��t��2\sqrt{3}��}\\{-{\frac{\sqrt{3}}{3}}^{t2}-6t+9\sqrt{3}��2\sqrt{3}��t��3\sqrt{3}��}\end{array}\right.$��
��3���ߡ�OCB=30�㣬���OCA��=60�㣬
��OC=PCʱ����POC=��OPC=75�㣬
���POA��=15�㣬
���ADE�Ƶ�O˳ʱ����ת15��ʱ����CPQΪ���������Σ�
��OP=PCʱ����NOC=OCP=30�㣬
���POC=30�㣬
�൱��ADE�Ƶ�O����ʱ����ת30��ʱ����CPQΪ���������Σ�
��OC=OP����OPC=��OCP-30�㣬
���POC=120�㣬
���POA��=60�㣬
�൱��ADE�Ƶ�O��˳ʱ����ת60��ʱ����CPQΪ���������Σ�
��OC=CP����COP=��CPO=15�㣬
���A��OP=75�㣬
�൱��ADE�Ƶ�O����ʱ����ת75��ʱ����CPQΪ���������Σ�
�൱��ADE�Ƶ�O˳ʱ����ת15�㣬��˳ʱ����ת60�㣬����ʱ����ת30�㣬����ʱ����ת75��ʱ����CPQΪ���������Σ�
���� ���⿼����ͼ�εı任-ƽ�ƣ����������ε����ʣ����������ε��ж������ʣ������ε�����ļ��㣬ע����������ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-4��-2 �� | B�� | ��2��-2 �� | C�� | ��-4��6 �� | D�� | ��2��6 �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
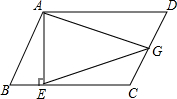 ��֪����?ABCD�У�AE��BC������ΪE����GΪCD�ϵ��е㣬
��֪����?ABCD�У�AE��BC������ΪE����GΪCD�ϵ��е㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪E��F�ֱ���������ABCD�ı�BC��CD�ϣ���AEƽ�֡�FAD����֤��BF+DE=AF��
��ͼ����֪E��F�ֱ���������ABCD�ı�BC��CD�ϣ���AEƽ�֡�FAD����֤��BF+DE=AF���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com