
【题目】甲、乙两城相距800千米,一辆客车从甲城开往乙城,车速为![]() 千米/小时,同时一辆出租车比乙城开往甲城,车速为90千米/小时.
千米/小时,同时一辆出租车比乙城开往甲城,车速为90千米/小时.
(1)设客车行驶时间为![]() (小时),当
(小时),当![]() 时,客车与乙城的距离为_______千米(用含
时,客车与乙城的距离为_______千米(用含![]() 的代数式表示);
的代数式表示);
(2)已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米.
,丙城在甲、乙两城之间,且与甲城相距260千米.
①求客车与出租车相距200千米时客车的行驶时间;(列方程解答)
②已知客车和出租车在甲、乙之间的![]() 处相遇时,出租车乘客小李突然接到开会通知,需要立即返回,此时小李有两种返回乙城的方案;
处相遇时,出租车乘客小李突然接到开会通知,需要立即返回,此时小李有两种返回乙城的方案;
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油的时间忽略不计;
方案二:在![]() 处换乘客车返回乙城.
处换乘客车返回乙城.
试通过计算,分析小李选择哪种方案能更快到达乙城?
【答案】(1)(800-3a);(2)小李选择方案一能更快到达乙城.
【解析】
(1)根据剩下的路程=总路程-已行驶的路程即可得到答案;
(2)①设当客车与出租车相距200千米时客车的行驶时间是![]() 小时,分相遇前、相遇后两种情况列方程解答;
小时,分相遇前、相遇后两种情况列方程解答;
②设客车和出租车x小时相遇,列方程求出x的值得到丙城与M处之间的距离为60km,再分别计算两种方案所需的时间即可得到答案.
(1)客车已行驶的路程是3a千米,
∴当![]() 时,客车与乙城的距离为(800-3a),
时,客车与乙城的距离为(800-3a),
故答案为:(800-3a);
(2)①设当客车与出租车相距200千米时客车的行驶时间是![]() 小时,
小时,
a:当客车和出租车没有相遇时,
60![]() +90
+90![]() +200=800 ,
+200=800 ,
解得![]() =4,
=4,
b:当客车和出租车相遇后,
60![]() +90
+90![]() -200=800,
-200=800,
解得:![]() =
=![]() ,
,
当客车与出租车相距200千米时客车的行驶时间是4小时或![]() 小时;
小时;
②设客车和出租车x小时相遇,
60x+90x=800 ,
∴x=![]() ,
,
此时客车走的路程为320km,出租车走的路程为480km,
∴丙城与M处之间的距离为60km,
方案一:小李需要的时间是(60+60+480)![]() 90=
90=![]() =
=![]() 小时;
小时;
方案二:小李需要的时间是480![]() 60=8小时.
60=8小时.
∵![]() <8,
<8,
∴小李选择方案一能更快到达乙城.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1是一座立交桥的示意图(道路宽度忽略不计), A为入口, F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF ;弯道为以点O为圆心的一段弧,且弧BC,弧ED,弧CD所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出. 其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法错误的是( )
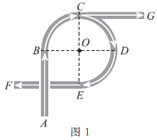

A. 甲车在立交桥上共行驶8s B. 从F口出比从G口出多行驶40m
C. 甲车从F口出,乙车从G口出 D. 立交桥总长为150m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
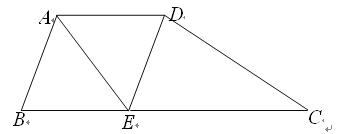
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°,CE=2BE,试判断△CDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
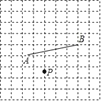
【题目】如图所示,在每个边长都为1的小正方形组成的网格中,点A、P分别为小正方形的中点,B为格点.
(I)线段AB的长度等于_____;
(Ⅱ)在线段AB上存在一个点Q,使得点Q满足∠PQA=45°,请你借助给定的网格,并利用不带刻度的直尺作出∠PQA,并简要说明你是怎么找到点Q的:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组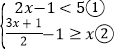
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
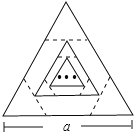
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]()
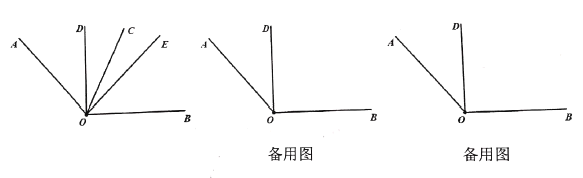
(1)求![]() ;
;
(2)![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转
的速度逆时针方向旋转![]() 秒(
秒(![]() ),
),![]() 为何值时
为何值时![]() ;
;
(3)射线![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转,射线
的速度逆时针方向旋转,射线![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度顺时针方向旋转,若射线
的速度顺时针方向旋转,若射线![]() 同时开始旋转
同时开始旋转![]() 秒(
秒(![]() )后得到
)后得到![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() (m为常数).
(m为常数).
(1)如果方程有两个不相等的实数根,求m的取值范围.
(2)如果方程有两个相等的实数根,求m的值。
(3)如果方程没有实数根,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com