练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．先化简，后求值：[$\frac{1}{a-2}$+$\frac{{a}^{2}-1}{（a+2）（a-1）}$]÷（$\frac{a}{a+2}$）2，其中a=2005．

    分析 原式先计算乘方运算，再计算除法运算，得到最简结果，把a的值代入计算即可求出值．

    解答 解：原式=（$\frac{1}{a-2}$+$\frac{a+1}{a+2}$）•$\frac{（a+2）^{2}}{{a}^{2}}$=$\frac{a+2+{a}^{2}-a-2}{（a+2）（a-2）}$•$\frac{（a+2）^{2}}{{a}^{2}}$=$\frac{{a}^{2}}{（a+2）（a-2）}$•$\frac{（a+2）^{2}}{{a}^{2}}$=$\frac{a+2}{a-2}$，
    当a=2015时，原式=$\frac{2015+2}{2015-2}$=$\frac{2017}{2013}$．

    点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

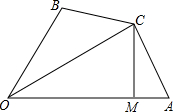    10．如图，在四边形OACB中，CM⊥OA于M，且CA=CB，∠OAC+∠OBC=180°，求证：
    （1）∠AOC=∠BOC；
    （2）OA+OB=2OM．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．已知a，b，c是△ABC的三边，则关于x的方程（a+b）x2-2cx+（a+b）=0的根的情况是（　　）
    A．没有实数根B．可能有且只有一个实数根
    C．有两个相等的实数根D．有两个不相等的实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知a=（-2）3，b=-$\sqrt{5}$+$\sqrt{\frac{9}{4}}$，c=$\root{3}{\frac{1}{8}}$，d=|2-$\sqrt{5}$|．
    （1）请化简a、b、c、d这四个数；
    （2）根据化简结果，求出这四个数中“有理数的和m”与“无理数的和n”，并比较m、n的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．根据下列问题，列出一元二次方程，并将其化成一般形式：
    （1）某班有x名同学，毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1980张照片．
    （2）一矩形面积为35cm2，长比宽多2cm，求这个矩形的长与宽．
    （3）把一块面积为54cm2的长方形纸片的一边剪下5cm，另一边剪下2cm，恰好变成一个正方形，求这个正方形的边长．
    （4）一个直角三角形的斜边长是17cm，两直角边之差为7cm，求较短直角边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．用合理的方法计算：7.52×1.6-2.52×1.6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算：|-2$\frac{1}{4}$|-（-$\frac{3}{4}$）+1-|1-$\frac{1}{2}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知三角形的三边长为a，b，c，根据三角形三边的关系化简：$\sqrt{（a+b+c）^{2}}$-$\sqrt{（a-b-c）^{2}}$=2a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，在平面直角坐标系中，反比例函数y1=$\frac{k_1}{x}$（x＞0）的图象与y2=$\frac{k_2}{x}$（x＞0）的图象关于x轴对称，Rt△AOB的顶点A，B分别在y1=$\frac{k_1}{x}$（x＞0）和y2=$\frac{k_2}{x}$（x＞0）的图象上．若OB=AB，点B的纵坐标为-2，则点A的坐标为（1+$\sqrt{5}$，3-$\sqrt{5}$）．

    查看答案和解析>>

    同步练习册答案