
| A. | 0 | B. | 1 | C. | 1008 | D. | 2016 |
分析 由(n+1)!=1×2×3×…×n×(n+1)=(n+1)×n!=n×n!+n!知,可将原式两边都加上1!+2!+3!+…+2016!,即可得S=2017!-1,所以S除以2017的余数是-1,再根据2017!能被2017整除,求出S除以2017的余数是多少即可.
解答 解:∵(n+1)!=1×2×3×…×n×(n+1)=(n+1)×n!=n×n!+n!,
∴S+1!+2!+3!+…+2016!=1×1!+2×2!+3×3!+…+2016×2016!+1!+2!+3!+…+2016!,
即S+1!+2!+3!+…+2016!=1!+2!+3!+…+2017!,
则S=2017!-1,
∵2017!能被2017整除,
∴S与1的和能被2017整除,
∴S除以2017的余数是:2017-1=2016.
故选:D.
点评 本题考查规律型:数字的变化类,解答此类问题的关键是弄清新定义,得出(n+1)!=(n+1)×n!=n×n!+n!的数据变化的规律是解题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
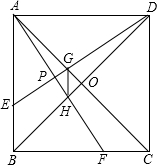 如图,已知在正方形ABCD中,AC与BD交与点O,E、F分别是AB、BC上的点,当点E、F在相同的时间、以相同的速度分别在AB、BC上从点A向B和从点B向C方向移动,是判断在E、F移动的期间:
如图,已知在正方形ABCD中,AC与BD交与点O,E、F分别是AB、BC上的点,当点E、F在相同的时间、以相同的速度分别在AB、BC上从点A向B和从点B向C方向移动,是判断在E、F移动的期间:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
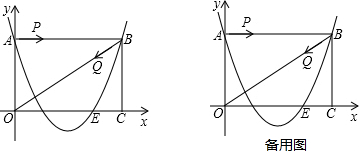
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com