
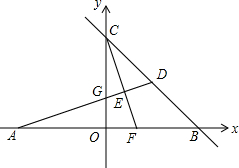
 如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.
如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.分析 (1)根据已知条件得到AB=8,B(4,0),C(0,4),待定系数法求得BC的解析式为y=-x+4,根据三角形的面积得到DH=2,即可得到结论;
(2)根据已知条件得到△AGO~△CGE,由相似三角形的性质得到∠GAO=∠GCE,根据全等三角形的性质即可得到结论;
(3)根据直线AD的解析式y=$\frac{1}{3}$x+$\frac{4}{3}$,求得OF=OG=$\frac{4}{3}$,①如图2,当∠CFP=90°,FP=FC时,过P作PH⊥x轴于H,根据全等三角形的性质得到PH=OF=$\frac{4}{3}$,FH=OC=4,于是得到P1($\frac{16}{3}$,$\frac{4}{3}$);②如图3,当∠PCF=90°,CP=FC时,根据全等三角形的性质得到PH=OC=4,CH=OF=$\frac{4}{3}$,于是得到P2(4,$\frac{16}{3}$);③如图4,当∠CPF=90°,PC=PF时,根据全等三角形的性质得到PN=PM,CN=FM,根据ON=OM,列方程得到CN=CM=$\frac{4}{3}$,于是得到P3($\frac{8}{3}$,$\frac{8}{3}$).
解答 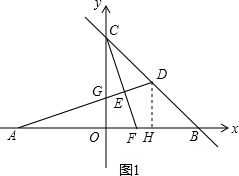 解:(1)如图1,作DH⊥x轴于H,
解:(1)如图1,作DH⊥x轴于H,
∵OA=OB=OC=4,
∴AB=8,B(4,0),C(0,4),
设BC的解析式为y=kx+b,
把B,C两点代入得$\left\{\begin{array}{l}{0=4k+b}\\{4=b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$,
∴BC的解析式为y=-x+4,
∵△ABD的面积为8,AB=8,
∴DH=2,
所以D点的纵坐标为2,
把y=2代入y=-x+4得:x=2,
∴D(2,2);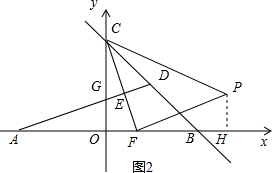
(2)∵CE⊥AD,
∴∠CEG=∠AOG=90°,
又∵∠AGO=∠CGE,
∴△AGO~△CGE,
∴∠GAO=∠GCE,
在△COF与△AOG中,$\left\{\begin{array}{l}{∠OCF=∠OAG}\\{OC=OA}\\{∠COF=∠AOG}\end{array}\right.$,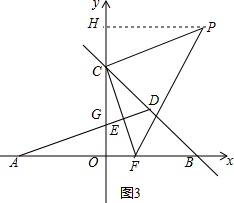 ∴△COF≌△AOG,
∴△COF≌△AOG,
∴OF=OG;
(3)存在,∵A(-4,0),D(2,2),
∴直线AD的解析式为y=$\frac{1}{3}$x+$\frac{4}{3}$,
∴OG=$\frac{4}{3}$,
∴OF=OG=$\frac{4}{3}$,
①如图2,当∠CFP=90°,FP=FC时,
过P作PH⊥x轴于H,
∴∠PHF=∠COF=90°,
∴∠OCF+∠OFC=∠OFC+∠PFH=90°,∴∠OCF=∠PFH,
在△COF与△PFH中,$\left\{\begin{array}{l}{∠OCF=∠PFH}\\{∠COF=∠PHF}\\{CF=PF}\end{array}\right.$,∴△COF≌△PFH,∴PH=OF=$\frac{4}{3}$,FH=OC=4,
∴OH=$\frac{16}{3}$,
∴P1($\frac{16}{3}$,$\frac{4}{3}$);
②如图3,当∠PCF=90°,CP=FC时,同理证得△PHC≌△CFO,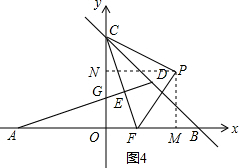
∴PH=OC=4,CH=OF=$\frac{4}{3}$,
∴OH=$\frac{16}{3}$,
∴P2(4,$\frac{16}{3}$);
③如图4,当∠CPF=90°,PC=PF时,
过P作PM⊥x轴于M,PN⊥y轴于N,
∴四边形PNOM是矩形,
∴∠NPM=90°,
∴∠CPN+∠NPF=∠NPF+∠FPM=90°,
∴∠CPN=∠FPM,
在△CPN与△FPM中,$\left\{\begin{array}{l}{∠CPN=∠FPM}\\{∠PNC=∠PMF=90°}\\{PC=PF}\end{array}\right.$,
∴△PNC≌△PMF,
∴PN=PM,CN=FM,
∴矩形PNOM是正方形,
∴ON=OM,
∴4-CN=$\frac{4}{3}$+CN,
∴CN=CM=$\frac{4}{3}$,
∴PN=PM=$\frac{8}{3}$,
∴P3($\frac{8}{3}$,$\frac{8}{3}$),
综上所述:P的坐标为($\frac{16}{3}$,$\frac{4}{3}$),(4,$\frac{16}{3}$),($\frac{8}{3}$,$\frac{8}{3}$).
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,矩形和正方形的判定和性质,待定系数法求函数的解析式,正确的作出辅助线构造全等三角形是解题的关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n.
如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
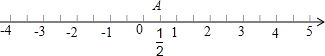 如图,数轴上点A表示$\frac{1}{2}$.
如图,数轴上点A表示$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
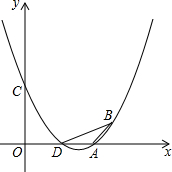 已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C.
已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com