
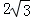 ,2)、C(0,4).
,2)、C(0,4).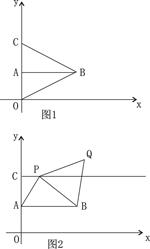
 的形状,并说明理由;
的形状,并说明理由;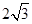 ;②等边三角形;(2)
;②等边三角形;(2)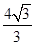 或0或
或0或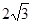 .
.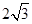 ,2)可得
,2)可得 ,在
,在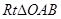 中,根据∠AOB的正切函数值即可得到
中,根据∠AOB的正切函数值即可得到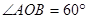 ,同理
,同理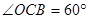 ,即可得到结果;
,即可得到结果;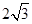 ;
;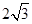 ,2)
,2)
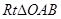 中,
中,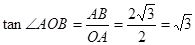
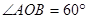 ,同理
,同理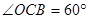
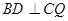 于D,则四边形
于D,则四边形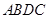 是矩形
是矩形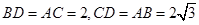
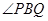
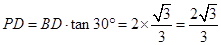
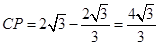
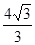 ;
;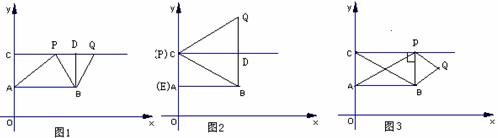
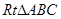 中,
中,
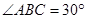 ,∵
,∵
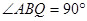 ,∴BQ∥AC,又CQ与AB不平行
,∴BQ∥AC,又CQ与AB不平行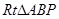 中,
中,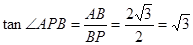
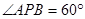
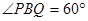

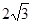
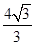 或0或
或0或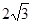 .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:不详 题型:填空题
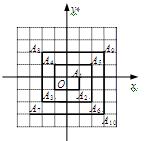
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
.
 的值;
的值;  轴上是否存在点C,使得△ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由;
轴上是否存在点C,使得△ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由;  是
是 轴正半轴上一点,且到
轴正半轴上一点,且到 轴的距离为3,若点
轴的距离为3,若点 沿
沿 轴负半轴方向以每秒1个长度单位平行移动至Q,当运动的时间
轴负半轴方向以每秒1个长度单位平行移动至Q,当运动的时间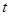 为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时Q点的坐标.
为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时Q点的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
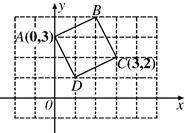
| A.(2,4) | B.(4,2) | C.(2,3) | D.不能确定 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com