
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点A.将直线
交于点A.将直线![]() 向右平移6个单位后,与双曲线
向右平移6个单位后,与双曲线![]() 交于点B,与x轴交于点C,若
交于点B,与x轴交于点C,若![]() ,则k的值为( )
,则k的值为( )
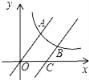
A. 12 B. 14 C. 18 D. 24
【答案】A
【解析】
试题作AD⊥x轴于D点,BE⊥x轴于E,根据平移得到C点坐标为(6,0),再证明Rt△AOD∽Rt△BCE,利用相似比得到OD=2CE,AD=2BE,设CE=t,则OD=2t,OE=6+t,然后表示A点坐标(2t,![]() ),B点坐标(6+t,
),B点坐标(6+t,![]() ),再根据反比例函数图象上点的坐标特征得到2t
),再根据反比例函数图象上点的坐标特征得到2t![]() =(6+t)
=(6+t)![]() ,解得t1=0(舍去),t2=2,于是A点坐标为(4,3),最后把A点坐标代入y=
,解得t1=0(舍去),t2=2,于是A点坐标为(4,3),最后把A点坐标代入y=![]() 即可确定k的值.
即可确定k的值.
试题解析:作AD⊥x轴于D点,BE⊥x轴于E,如图,
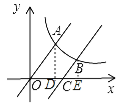
∵直线y=![]() 向右平移6个单位得到直线OC,
向右平移6个单位得到直线OC,
∴C点坐标为(6,0),
∵OA∥BC,
∴∠AOD=∠BCE,
∴Rt△AOD∽Rt△BCE,
∴![]() ,
,
∴OD=2CE,AD=2BE,
设CE=t,则OD=2t,OE=6+t,
当x=2t时,y=![]() ,即A点坐标为(2t,
,即A点坐标为(2t,![]() )
)
∴BE=![]() ,
,
∴B点坐标为(6+t,![]() ),
),
∴2t![]() =(6+t)
=(6+t)![]() ,
,
解得t1=0(舍去),t2=2,
∴A点坐标为(4,3),
把A点坐标为(4,3)代入y=![]() 得k=3×4=12.
得k=3×4=12.
故选A.


科目:初中数学 来源: 题型:
【题目】给出下列命题及函数y=﹣x,y=﹣x2,y=![]() 的图象.①如果﹣a>﹣
的图象.①如果﹣a>﹣![]() >﹣a2,那么a<﹣1;②如果﹣
>﹣a2,那么a<﹣1;②如果﹣![]() >﹣a2>﹣a,那么﹣1<a<0;③如果﹣a2>﹣a>﹣
>﹣a2>﹣a,那么﹣1<a<0;③如果﹣a2>﹣a>﹣![]() ,那么0<a<1;④如果﹣
,那么0<a<1;④如果﹣![]() >﹣a2>﹣a.那么a>1,则正确命题的序号是( )
>﹣a2>﹣a.那么a>1,则正确命题的序号是( )
A. ①② B. ②③ C. ①③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() +n(n<0)与坐标轴交于A、B两点,与y=
+n(n<0)与坐标轴交于A、B两点,与y=![]() (x>0)交于点E,过点E作EF⊥x轴,垂足为F,且△OAB∽△FEB,相似比为
(x>0)交于点E,过点E作EF⊥x轴,垂足为F,且△OAB∽△FEB,相似比为![]() .
.
(1)若n=-![]() ,求m的值;
,求m的值;
(2)连接OE,试探究m与n的数量关系,并直接写出直线OE的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名同学推铅球,铅球出手后行进过程中离地面的高度![]() (单位:
(单位:![]() )与水平距离
)与水平距离![]() (单位:
(单位:![]() )近似满足函数关系
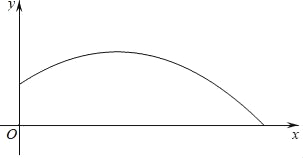
)近似满足函数关系![]() ,其图象如图所示.已知铅球落地时的水平距离为
,其图象如图所示.已知铅球落地时的水平距离为![]() .
.
(1)求铅球出手时离地面的高度;
(2)在铅球行进过程中,当它离地面的高度为![]() 时,求此时铅球的水平距离.
时,求此时铅球的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
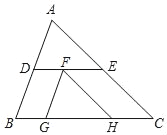
【题目】如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,点F在线段DE上,过点F作FG∥AB、FH∥AC分别交BC于点G、H,如果BG:GH:HC=2:4:3.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
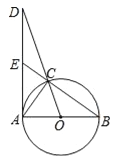
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
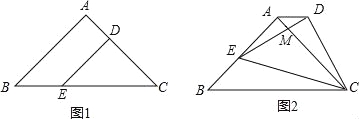
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=2![]() ,D、E两点分别在AC、BC上,且DE∥AB,DC=2
,D、E两点分别在AC、BC上,且DE∥AB,DC=2![]() ,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
,将△CDE绕点C顺时针旋转得到△CD′E′,如图2,点D、E对应点分别为D′、E′、D′、E′与AC相交于点M,当E′刚好落在边AB上时,△AMD′的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
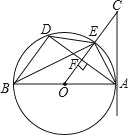
【题目】如图,AB是⊙O的直径,AC切⊙O于点A,AD是⊙O的弦,OC⊥AD于F交⊙O于E,连接DE,BE,BD,AE.
(1)求证:∠C=∠BED;
(2)如果AB=10,tan∠BAD=![]() ,求AC的长;
,求AC的长;
(3)如果DE∥AB,AB=10,求四边形AEDB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com