
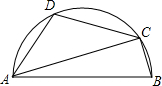
 如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,$\widehat{AD}$=$\widehat{CD}$,求:∠BCD的度数.
如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,$\widehat{AD}$=$\widehat{CD}$,求:∠BCD的度数. 分析 连结BC,如图,根据圆周角定理得∠ACB=90°,则利用互余可计算出∠B=70°,再根据圆内接四边形的性质计算出∠D=180°-∠B=110°,接着根据圆周角定理和三角形内角和定理,由弧AD=弧CD得到∠DAC=∠DCA=35°,然后得到∠DCB=∠DCA+∠ACB=125°.
解答 解:连结BC,如图,
∵AB是半圆的直径,
∴∠ACB=90°,
∵∠BAC=20°,
∴∠B=70°,
∵四边形ABCD是圆O的内接四边形,
∴∠D=180°-∠B=110°,
∵$\widehat{AD}$=$\widehat{CD}$,
∴∠DAC=∠DCA=$\frac{1}{2}$(180°-110°)=35°,
∴∠DCB=∠DCA+∠ACB=125°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了圆内接四边形的性质.


科目:初中数学 来源: 题型:解答题
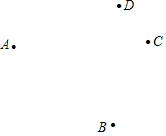 已知平面上A,B,C,D四个点,按下列要求画出图形.
已知平面上A,B,C,D四个点,按下列要求画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
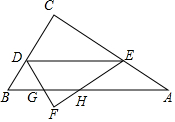 直角三角形ABC中,∠C=90度,CB=6,AC=8,D为CB边上一个动点,E为AC上一点,DE∥AB,将三角形CDE沿着DE翻折得到三角形DEF,设三角形DEF和三角形ABC重合的面积为y,DC=x,求y与x的函数关系式及定义域.
直角三角形ABC中,∠C=90度,CB=6,AC=8,D为CB边上一个动点,E为AC上一点,DE∥AB,将三角形CDE沿着DE翻折得到三角形DEF,设三角形DEF和三角形ABC重合的面积为y,DC=x,求y与x的函数关系式及定义域.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
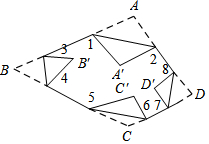 如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.
如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com