
【题目】如图所示,△ABC为等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,有下列四个结论:①点P在∠BAC的平分线上;②AS=AR;③QP∥AB;④△BRP≌△CSP.其中,正确的有__________(填序号即可).

【答案】①②③④
【解析】
根据角平分线性质即可推出①,根据勾股定理即可推出AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出QP∥AB即可;根据HL推出△BRP≌△CSP即可.
∵PR⊥AB于点R,PS⊥AC,PR=PS,∴点P在∠A的平分线上,∴①正确;
∵点P在∠A的平分线上,∴∠QAP=∠BAP.
在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2﹣PR2,AS2=AP2﹣PS2.
∵AP=AP,PR=PS,∴AR=AS,∴②正确;
∵AQ=QP,∴∠QAP=∠QPA.
∵∠QAP=∠BAP,∴∠QPA=∠BAP,∴QP∥AB ,∴③正确;
∵△ABC是等边三角形,∴∠B=∠CAB=60°,AB=AC.
∵∠QAP=∠BAP,∴BP=CP.
∵PR⊥AB,PS⊥AC,∴∠BRP=∠PSQ=90°.
在Rt△BRP和Rt△CSP中,∵BP=CP,PR=PS,∴△BRP≌△CSP,∴④正确.
故选A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线![]() 和
和![]() 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(![]() ,
, ![]() ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ABC=90°,AB=BC,点D是AC的中点,直角∠EDF的两边分别交AB、BC于点E、F,给出以下结论:①AE=BF;②S四边形BEDF=![]() S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
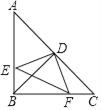
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝建校八十周年,某校各班都在开展丰富多彩的庆祝活动,八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的长方形纸片ABCD;②将纸片沿着直线AE折叠,使点D恰好落在BC边上的F处……请你根据①②步骤解答下列问题.

(1)找出图中的∠FEC的余角;
(2)计算EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( ) 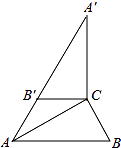
A.4 ![]()
B.6
C.3 ![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆旅游车从大理返回昆明,旅游车到昆明的距离y(km)与行驶时间x(h)之间的函数关系如图所示,试回答下列问题:
(1)求距离y(km)与行驶时间x(h)的函数表达式(不求自变量的取值范围);
(2)若旅游车8:00从大理出发,11:30在某加油站加油,问此时旅游车距离昆明还有多远(途中停车时间不计)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在菱形ABCD中,∠ABC=60°,M、N分别是边BC,CD上的两个动点,∠MAN=60°,AM、AN分别交BD于E、F两点.

(1)如图1,求证:CM+CN=BC;
(2)如图2,过点E作EG∥AN交DC延长线于点G,求证:EG=EA;
(3)如图3,若AB=1,∠AED=45°,直接写出EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com