
 药品研究所开发一种抗菌新药,经过多年的动物实验后,首次用于临床人体试验,测得成人服药后血液中的药物浓度y(μg/ml)与服药后时间x(h)之间的函数关系如图所示,则当1≤x≤6时,y的取值范围是( )
药品研究所开发一种抗菌新药,经过多年的动物实验后,首次用于临床人体试验,测得成人服药后血液中的药物浓度y(μg/ml)与服药后时间x(h)之间的函数关系如图所示,则当1≤x≤6时,y的取值范围是( )| A. | $\frac{8}{3}$≤y≤$\frac{64}{11}$ | B. | $\frac{64}{11}$≤x≤8 | C. | $\frac{8}{3}$≤y≤8 | D. | 8≤x≤16 |
分析 根据题意和函数图象分别求得相应的函数解析式,再将x=1和x=6代入相应的函数解析式即可求得y的取值范围.
解答 解:设当0≤x≤3时,y与x的函数关系式为y=kx,
3k=8,得k=$\frac{8}{3}$,
∴当0≤x≤3时,y与x的函数关系式为y=$\frac{8}{3}x$,
∴当x=1时,y=$\frac{8}{3}$,
设当3≤x≤14时,y与x的函数关系式为y=ax+b,
$\left\{\begin{array}{l}{3a+b=8}\\{14a+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{a=-\frac{8}{11}}\\{b=\frac{112}{11}}\end{array}\right.$,
即当3≤x≤14时,y与x的函数关系式为y=$-\frac{8}{11}x+\frac{112}{11}$,
则当x=6时,y=$-\frac{8}{11}×6+\frac{112}{11}$=$\frac{64}{11}$,
∵$\frac{8}{3}<\frac{64}{11}$,当1≤x≤6时,y的最大值是8,
∴y的取值范围是$\frac{8}{3}≤y≤8$,
故选C.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质和数形结合的思想解答.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
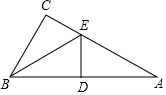 如图,在△ABC中,∠C是直角,将△BCE沿BE翻折,点C恰好落在边AB的中点D的位置上;再沿ED翻折,△ADE恰好与△BDE重合,写出图中所有的全等三角形,图中与∠A对应相等的有哪些角?与线段BC对应相等的有哪些线段?
如图,在△ABC中,∠C是直角,将△BCE沿BE翻折,点C恰好落在边AB的中点D的位置上;再沿ED翻折,△ADE恰好与△BDE重合,写出图中所有的全等三角形,图中与∠A对应相等的有哪些角?与线段BC对应相等的有哪些线段?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF中,∠ECF=90°,面积为200,则BE的值为12.
如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF中,∠ECF=90°,面积为200,则BE的值为12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
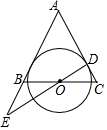 如图,在△ABC中,AB=AC,点O为BC中点,⊙O与AC相切于点D,连接DO并延长,与AB的延长线相交于点E.
如图,在△ABC中,AB=AC,点O为BC中点,⊙O与AC相切于点D,连接DO并延长,与AB的延长线相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
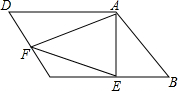 已知:在平行四边形ABCD中,AE⊥BC,垂足为E,点F为CD的中点,连接AF,EE.
已知:在平行四边形ABCD中,AE⊥BC,垂足为E,点F为CD的中点,连接AF,EE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -3 | -2 | -1 | $-\frac{1}{2}$ | $-\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | $-\frac{1}{2}$ | $-\frac{15}{8}$ | -$\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
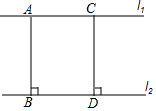 如图,直线l1∥l2,过l1上两点A,C分别作AB⊥l2,CD⊥l2,则下列说法正确的是( )
如图,直线l1∥l2,过l1上两点A,C分别作AB⊥l2,CD⊥l2,则下列说法正确的是( )| A. | AB>CD | B. | AB<CD | C. | AB=CD | D. | D、 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com