
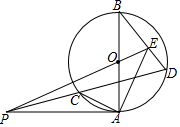
 如图,AB为⊙O直径,PA切⊙O于A,PCD为⊙O一条割线,PO交BD于E,证明:AC⊥AE.
如图,AB为⊙O直径,PA切⊙O于A,PCD为⊙O一条割线,PO交BD于E,证明:AC⊥AE. 分析 连接BC交PE于F,连接AF,过C作CH∥PE分别交AB,BD于G,H,过O作OM⊥PD于M,连接GM,AM,根据切线的性质得到AB⊥AP,推出P,O,M,A四点共圆,根据圆周角定理得到∠EPD=∠OAM,根据平行线的性质得到∠HCD=∠EPD,于是得到∠GOM=∠GAM,推出G,CA,M四点共圆,根据圆周角定理得到∠CMG=∠CAB,等量代换得到∠CMG=∠CDB,根据平行线的判定定理得到GM∥BD,推出四边形AEBF是平行四边形,根据平行线的性质即可得到结论.
解答 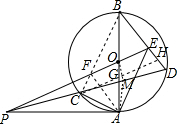 证明:连接BC交PE于F,连接AF,过C作CH∥PE分别交AB,BD于G,H,过O作OM⊥PD于M,连接GM,AM,
证明:连接BC交PE于F,连接AF,过C作CH∥PE分别交AB,BD于G,H,过O作OM⊥PD于M,连接GM,AM,
∵AB为⊙O直径,PA切⊙O于A,
∴AB⊥AP,
∵OM⊥PD,
∴P,O,M,A四点共圆,
∴∠EPD=∠OAM,
∵CH∥PE,
∴∠HCD=∠EPD,
∴∠HCD=∠OAM,
即∠GOM=∠GAM,
∴G,C,A,M四点共圆,
∴∠CMG=∠CAB,
∵∠CAB=∠CDB,
∴∠CMG=∠CDB,
∴GM∥BD,
∵OM⊥PD,
∴CM=DM,
∴CG=HG,
∵CH∥PE,
∴FO=EO,
∵AO=BO,
∴四边形AEBF是平行四边形,
∴BC∥AE,
∴∠BCA+∠CAE=180°,
∵∠BCA=90°,
∴∠CAE=90°,
∴AC⊥AE.
点评 本题考查了切线的性质,四点共圆,圆周角定理,平行线的性质,正确的作出辅助线是解题的关键.


 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
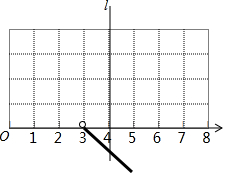 如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线l对称的点,如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹.
如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线l对称的点,如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m.设AD的长为x m,菜园ABCD的面积为y m2.则函数y关于自变量x的函数关系式是y=(30-2x)x,x的取值范围是6≤x<15.
如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m.设AD的长为x m,菜园ABCD的面积为y m2.则函数y关于自变量x的函数关系式是y=(30-2x)x,x的取值范围是6≤x<15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
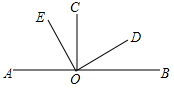 如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角)
如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com