
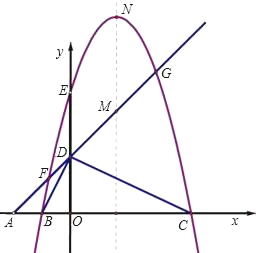
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
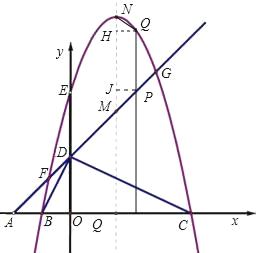
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
【答案】(1)y=﹣x2+3x+4;(2)△BDC是直角三角形,证明见解析;△POC是等腰三角形时,点P坐标是(﹣1+![]() ,1+
,1+![]() )或(2,4);(3)①不能成为菱形,理由见解析;②能成为等腰梯形,点P的坐标是(2.5,4.5).
)或(2,4);(3)①不能成为菱形,理由见解析;②能成为等腰梯形,点P的坐标是(2.5,4.5).
【解析】
(1)利用待定系数法列方程组求二次函数的解析式.(2)利用勾股定理的逆定理,判断直角三角形.(3)分别设出P,Q点坐标,按照菱形的条件,等腰梯形的条件,分别求P点坐标,判断是否存在.
(1)B(﹣1,0)E(0,4)C(4,0)设解析式是y=ax2+bx+c,
可得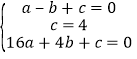 ,
,
解得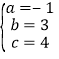 ,
,
∴y=﹣x2+3x+4;
(2)△BDC是直角三角形,
∵BD2=BO2+DO2=5,DC2=DO2+CO2=20,BC2=(BO+CO)2=25
∴BD2+DC2=BC2,
∴△BDC是直角三角形.
点A坐标是(﹣2,0),点D坐标是(0,2),
设直线AD的解析式是y=kx+b,则![]() ,
,
解得:![]() ,
,
则直线AD的解析式是y=x+2,
设点P坐标是(x,x+2)
当OP=OC时x2+(x+2)2=16,
解得:x=﹣1±![]() (x=﹣1-
(x=﹣1-![]() (不符合,舍去)此时点P(﹣1+
(不符合,舍去)此时点P(﹣1+![]() ,1+
,1+![]() )
)
当PC=OC时(x+2)2+(4﹣x)2=16,方程无解;
当PO=PC时,点P在OC的中垂线上,
∴点P横坐标是2,得点P坐标是(2,4);
∴当△POC是等腰三角形时,点P坐标是(﹣1+![]() ,1+
,1+![]() )或(2,4);
)或(2,4);
(3)点M坐标是(![]() ,
,![]() ),点N坐标是(
),点N坐标是(![]() ,
,![]() ),∴MN=
),∴MN=![]() ,
,
设点P为(x,x+2),Q(x,﹣x2+3x+4),则PQ=﹣x2+2x+2
①若PQNM是菱形,则PQ=MN,可得x1=0.5,x2=1.5
当x2=1.5时,点P与点M重合;当x1=0.5时,可求得PM=![]() 所以菱形不存在.
所以菱形不存在.
②能成为等腰梯形,作QH⊥MN于点H,作PJ⊥MN于点J,则NH=MJ,
则![]() ﹣(﹣x2+3x+4)=x+2﹣
﹣(﹣x2+3x+4)=x+2﹣![]() ,
,
解得:x=2.5,
此时点P的坐标是(2.5,4.5).


科目:初中数学 来源: 题型:
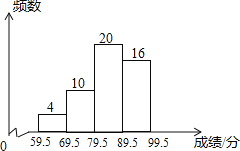
【题目】为增强学生环保意识,某中学组织全校3000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如下统计图.
请根据图中提供的信息,解答下列问题:
(1)若抽取的成绩用扇形图来描述,则表示“第二组(69.5~79.5)”的扇形的圆心角 度;
(2)若成绩在90分以上(含90分)的同学可获奖,请估计该校约有多少名同学获奖?
(3)某班准备从成绩最好的4名同学(男、女各2名)中随机选取2名同学去社区进行环保宣传,则选出的同学恰好是1男1女的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(k-2)x2-4x+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
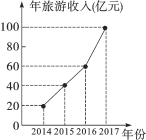
【题目】某人为了解他所在地区的旅游情况,收集了该地区2014年到2017年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
(1)该地区2014年到2017年四年的年旅游平均收入是多少亿元;
(2)从折线统计图中你能获得哪些信息?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
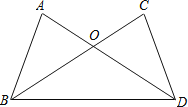
【题目】(1)如图,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
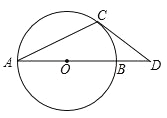
(2)如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD=![]() ,求∠BAC的度数.
,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是一块绿化带,阴影部分EOFB,GHMN都是正方形的花圃,其中EOFB的顶点O是正方形中心.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
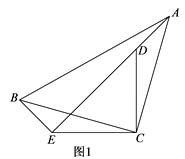
【题目】已知等腰RtABC与等腰RtCDE,∠ACB=∠DCE=90°.把RtABC绕点C旋转.
(1)如图1,当点A旋转到ED的延长线时,若![]() ,BE=5,求CD的长;
,BE=5,求CD的长;
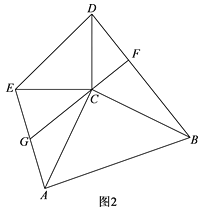
(2)当RtABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com