
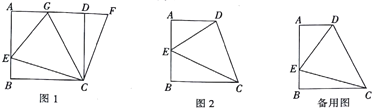
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚÕż·½ŠĪABCDÖŠ£¬µćEŹĒABÉĻŅ»µć£¬µćFŹĒADŃÓ³¤ĻßÉĻŅ»µć£¬ĒŅDF=BE£¬Į¬½ÓCE”¢CF£®
£Ø1£©ĒóÖ¤£ŗCE=CF£®
£Ø2£©ŌŚĶ¼1ÖŠ£¬ČōµćGŌŚADÉĻ£¬ĒŅ”ĻGCE=45”ć£¬ŌņGE=BE+GD³ÉĮ¢Āš£æĪŖŹ²Ć“£æ
£Ø3£©øł¾ŻÄćĖłŃ§µÄÖŖŹ¶£¬ŌĖÓĆ£Ø1£©”¢£Ø2£©½ā“šÖŠ»żĄŪµÄ¾Ń飬Ķź³ÉĻĀĮŠø÷Ģā£¬ČēĶ¼2£¬ŌŚĖıߊĪABCDÖŠ£¬AD”ĪBC£ØBC£¾AD£©£¬”ĻB=90”ć£¬AB=BC£¬ĒŅ”ĻDCE=45”ć£®
¢ŁČōAE=6£¬DE=10£¬ĒóABµÄ³¤£»
¢ŚČōAB=BC=9£¬BE=3£¬ĒóDEµÄ³¤£®
”¾“š°ø”æ£Ø1£©Ö¤Ć÷¼ū½āĪö£Ø2£©³ÉĮ¢£Ø3£©¢Ł12£»¢Ś7.5
”¾½āĪö”æ
£Ø1£©ĻČÅŠ¶Ļ³ö”ĻB=”ĻCDF£¬½ų¶ųÅŠ¶Ļ³ö”÷CBE”Õ”÷CDE£¬¼“æÉµĆ³ö½įĀŪ£»
£Ø2£©ĻČÅŠ¶Ļ³ö”ĻBCE=”ĻDCF£¬½ų¶ųÅŠ¶Ļ³ö”ĻECF=”ĻBCD=90”ć£¬¼“æÉµĆ³ö”ĻGCF=”ĻGCE=45”ć£¬µĆ³ö”÷ECG”Õ”÷FCG¼“æÉµĆ³ö½įĀŪ£»
£Ø3£©ĻČÅŠ¶Ļ³ö¾ŲŠĪABCHĪŖÕż·½ŠĪ£¬½ų¶ųµĆ³öAH=BC=AB£¬
¢Łøł¾Ż¹“¹É¶ØĄķµĆ£¬AD=8£¬ÓÉ£Ø1£©£Ø2£©ÖŖ£¬ED=BE+DH£¬ÉčBE=x£¬½ų¶ų±ķŹ¾³öDH=10-x£¬ÓĆAH=AB½ØĮ¢·½³Ģ¼“æÉµĆ³ö½įĀŪ£»
¢ŚÓÉ£Ø1£©£Ø2£©ÖŖ£¬ED=BE+DH£¬ÉčDE=a£¬½ų¶ų±ķŹ¾³öDH=a-3£¬AD=12-a£¬AE=6£¬øł¾Ż¹“¹É¶ØĄķ½ØĮ¢·½³ĢĒó½ā¼“æÉµĆ³ö½įĀŪ£®
£Ø1£©ŌŚÕż·½ŠĪABCDÖŠ£¬
”ßBC=CD£¬”ĻB=”ĻADC£¬
”ą”ĻB=”ĻCDF£¬
”ßBE=DF£¬
”ą”÷CBE”Õ”÷CDF£¬
”ąCE=CF£»
£Ø2£©³ÉĮ¢£¬ÓÉ£Ø1£©ÖŖ£¬”÷CBF”Õ”÷CDE£¬
”ą”ĻBCE=”ĻDCF£¬
”ą”ĻBCE+”ĻECD=”ĻDCF+”ĻECD£¬
”ą”ĻECF=”ĻBCD=90”ć£¬
”ß”ĻGCE=45”ć£¬
”ą”ĻGCF=”ĻGCE=45”ć£¬
”ßCE=CF£¬”ĻGCE=”ĻGCF£¬GC=GC£¬
”ą”÷ECG”Õ”÷FCG£¬
”ąGE=GF£¬
”ąGE=DF+GD=BE+GD£»
£Ø3£©ČēĶ¼2£¬¹żµćC×÷CH”ĶAD½»ADµÄŃÓ³¤ĻßÓŚH£¬
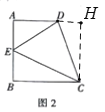
”ßAD”ĪBC£¬”ĻB=90”ć£¬
”ą”ĻA=90”ć£¬
”ß”ĻCHA=90”ć£¬
”ąĖıߊĪABCHĪŖ¾ŲŠĪ£¬
”ßAB=BC£¬
”ą¾ŲŠĪABCHĪŖÕż·½ŠĪ£¬
”ąAH=BC=AB£¬
¢Ł”ßAE=6£¬DE=10£¬øł¾Ż¹“¹É¶ØĄķµĆ£¬AD=8£¬
”ß”ĻDCE=45”ć£¬
ÓÉ£Ø1£©£Ø2£©ÖŖ£¬ED=BE+DH£¬
ÉčBE=x£¬
”ą10+x=DH£¬
”ąDH=10-x£¬
”ßAH=AB£¬
”ą8+10-x=x+6£¬
”ąx=6£¬
”ąAB=12£»
¢Ś”ß”ĻDCE=45”ć£¬
ÓÉ£Ø1£©£Ø2£©ÖŖ£¬ED=BE+DH£¬
ÉčDE=a£¬
”ąa=3+DH£¬
”ąDH=a-3£¬
”ßAB=AH=9£¬
”ąAD=9-£Øa-3£©=12-a£¬AE=AB-BE=6£¬
øł¾Ż¹“¹É¶ØĄķµĆ£¬DE2=AD2+AE2£¬
¼“£ŗ£Ø12-a£©2+62=a2£¬”ąa=7.5£¬
”ąDE=7.5£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬OŹĒµČ±ß”÷ABCÄŚŅ»µć£¬OA=3£¬OB=4£¬OC=5£¬½«Ļ߶ĪBOŅŌµćBĪŖŠż×ŖÖŠŠÄÄꏱÕėŠż×Ŗ60”ćµĆµ½Ļ߶ĪBO”䣬ĻĀĮŠ½įĀŪ£ŗ
¢Ł”÷BO”äAæÉŅŌÓÉ”÷BOCČʵćBÄꏱÕėŠż×Ŗ60”ćµĆµ½£»
¢ŚµćOÓėO”äµÄ¾ąĄėĪŖ4£»
¢ŪĖıߊĪAO BO”äµÄĆ껿ĪŖ6+3 ![]()
¢Ü”ĻAOB=150”ć£»
¢ŻS”÷AOC+S”÷AOB=6+ ![]() £®
£®
ĘäÖŠÕżČ·µÄ½įĀŪŹĒ£Ø £©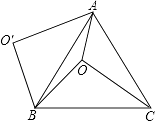
A.¢Ś¢Ū¢Ü¢Ż
B.¢Ł¢Ū¢Ü¢Ż
C.¢Ł¢Ś¢Ū¢Ż
D.¢Ł¢Ś¢Ü¢Ż
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij·ž×°³§¼Ę»®ČōøÉĢģĶź³ÉŅ»Åś¼ŠæĖÉĄµÄ¶©»õČĪĪń£®Čē¹ūĆæĢģÉś²ś·ž×° 20 ¼ž£¬ÄĒĆ“¾Ķ±Č¶©»õČĪĪńÉŁÉś²ś 100 ¼ž£»Čē¹ūĆæĢģÉś²ś 23 ¼ž£¬ÄĒĆ“¾Ķæɳ¬¹ż¶©»õČĪĪń 20 ¼ž£®
£Ø1£©ČōÉčŌ¼Ę»® x ĢģĶź³É£¬ŌņÕāÅś¼ŠæĖÉĄµÄ¶©»õČĪĪńÓĆ x µÄ“śŹżŹ½æɱķŹ¾ ĪŖ £®øł¾ŻĢāŅāĮŠ³ö·½³Ģ£¬²¢Ēó³öŌ¼Ę»®¶ąÉŁĢģĶź³É£æÕāÅś¼ŠæĖÉĄµÄ¶©»õČĪĪńŹĒ¶ąÉŁ£æ
£Ø2£©ČōÉčÕāÅś¼ŠæĖÉĄµÄ¶©»õČĪĪńĪŖ y ¼ž£¬ŹŌøł¾ŻĢāŅāĮŠ³ö·½³Ģ£®£ØÖ±½ÓĮŠ³ö·½³Ģ£¬²»±ŲĒó½ā£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±ĻßABµÄ½āĪöŹ½ĪŖy=![]() x+4£¬ÓėyÖį½»ÓŚµćA£¬ÓėxÖį½»ÓŚµćB£¬µćPĪŖĻ߶ĪABÉĻµÄŅ»øö¶Æµć£¬×÷PE”ĶyÖįÓŚµćE£¬PF”ĶxÖįÓŚµćF£¬Į¬½ÓEF£¬ŌņĻ߶ĪEFµÄ×īŠ”ÖµĪŖ_____£®
x+4£¬ÓėyÖį½»ÓŚµćA£¬ÓėxÖį½»ÓŚµćB£¬µćPĪŖĻ߶ĪABÉĻµÄŅ»øö¶Æµć£¬×÷PE”ĶyÖįÓŚµćE£¬PF”ĶxÖįÓŚµćF£¬Į¬½ÓEF£¬ŌņĻ߶ĪEFµÄ×īŠ”ÖµĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖÅ×ĪļĻß¾¹żA£Ø©4£¬0£©£¬B£Ø0£¬©4£©£¬C£Ø2£¬0£©Čżµć£® 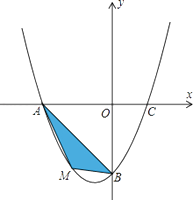
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ČōµćMĪŖµŚČżĻóĻŽÄŚÅ×ĪļĻßÉĻŅ»¶Æµć£¬µćMµÄŗį×ų±źĪŖm£¬”÷AMBµÄĆ껿ĪŖS£®ĒóS¹ŲÓŚmµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öSµÄ×ī“óÖµ£®
£Ø3£©ČōµćPŹĒÅ×ĪļĻßÉĻµÄ¶Æµć£¬µćQŹĒÖ±Ļßy=©xÉĻµÄ¶Æµć£¬ÅŠ¶ĻÓŠ¼øøöĪ»ÖĆÄܹ»Ź¹µĆµćP”¢Q”¢B”¢OĪŖ¶„µćµÄĖıߊĪĪŖĘ½ŠŠĖıߊĪ£¬Ö±½ÓŠ“³öĻąÓ¦µÄµćQµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(1)½ā²»µČŹ½2(x£«1)£1”Ż3x£«2£¬²¢°ŃĖüµÄ½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£»
(2)½ā²»µČŹ½![]() £1”Ż
£1”Ż![]() £¬²¢½«½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£®
£¬²¢½«½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øö²»ĶøĆ÷µÄæŚ“üĄļ×°ÓŠ·Ö±š±źÓŠŗŗ×Ö”°ŠŅ”±”¢”°ø£”±”¢”°ĮÄ”±”¢”°³Ē”±µÄĖÄøöŠ”Ēņ£¬³żŗŗ×Ö²»Ķ¬Ö®Ķā£¬Š”ĒņƻӊČĪŗĪĒų±š£¬Ćæ“ĪĆžĒņĒ°ĻČ½Į°č¾łŌČŌŁĆžĒņ£®
£Ø1£©Čō“ÓÖŠČĪČ”Ņ»øöĒņ£¬ĒņÉĻµÄŗŗ×ÖøÕŗĆŹĒ”°ø£”±µÄøÅĀŹĪŖ¶ąÉŁ£æ
£Ø2£©Š”Ó±“ÓÖŠČĪČ”Ņ»Ēņ£¬¼ĒĻĀŗŗ×Öŗó·Å»Ų“üÖŠ£¬Č»ŗóŌŁ“ÓÖŠČĪČ”Ņ»Ēņ£¬ĒóŠ”ӱȔ³öµÄĮ½øöĒņÉĻŗŗ×ÖĒ”ÄÜ×é³É”°ŠŅø£”±»ņ”°ĮijĒ”±µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓĆĮ½ÖÖÕż¶ą±ßŠĪĘĢĀśµŲĆę£¬ĘäÖŠŅ»ÖÖŹĒÕż°Ė±ßŠĪ£¬ŌņĮķŅ»ÖÖÕż¶ą±ßŠĪŹĒ£Ø £©”£
A. ÕżČż½ĒŠĪ B. ÕżĖıߊĪ C. ÕżĪå±ßŠĪ D. ÕżĮł±ßŠĪ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ABŹĒ”ŃOÖ±¾¶£¬OD”ĶĻŅBCÓŚµćF£¬ĒŅ½»”ŃOÓŚµćE£¬Čō”ĻAEC=”ĻODB£® 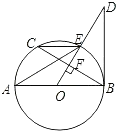
£Ø1£©ÅŠ¶ĻÖ±ĻßBDŗĶ”ŃOµÄĪ»ÖĆ¹ŲĻµ£¬²¢øų³öÖ¤Ć÷£»
£Ø2£©µ±AB=10£¬BC=8Ź±£¬ĒóBDµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com