Question

已知：图1，点P在线段AB上(AP＞PB)，C、D、E分别是AP、PB、AB的中点，正方形CPFG和正方形PDHK在直线AB同侧．

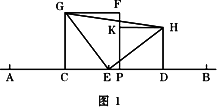
(1)求证：△EHG是等腰直角三角形；

(2)若将图1中的射线PB连同正方形PDHK绕点P顺时针旋转一个角度后，其它已知条件不变，图2，判断△EHG还是等腰直角三角形吗？请说明理由．

Answer 1

答案：
解析：

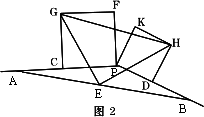
(1)证明：∵C、D、E分别是AP、PB、AB的中点， 　　∴CE＝AE－AC＝AB－AP＝(AB－AP)＝BP＝DP．1分 　　∴CE＋EP＝DP＋EP，即CP＝DE． 　　∵四边形CPFG和PDHK都是正方形， 　　∴在△CEG和△DHE中， 　　CE＝DP＝DH，CG＝CP＝DE，∠GCE＝∠EDH＝90°． 　　∴△CEG≌△DHE．2分 　　∴EG＝HE，∠EGC＝∠HED 　　而∠EGC＋∠CEG＝90°， 　　∴∠HED＋∠CEG＝90°． 　　∴∠GEH＝90°． 　　又∵EG＝HE， 　　∴△EHG是等腰直角三角形．3分 　　(2)△EHG还是等腰直角三角形．4分 　　理由如下： 　　联结CE、ED，得□CEDP， 　　可知∠PCE＝∠PDE． 　　进而得∠GCE＝∠EDH， 　　再由CE＝BP＝DP＝DH， 　　CG＝CP＝AP＝DE， 　　仍可证△CEG≌△DHE．5分 　　∴EG＝HE，∠EGC＝∠HED 　　如图，设EG和CP相交于M， 　　则∠GEH＝∠GED－∠HED， 　　＝∠GMP－∠EGC 　　＝∠GCM 　　＝90° 　　∴△EHG是等腰直角三角形．6分