
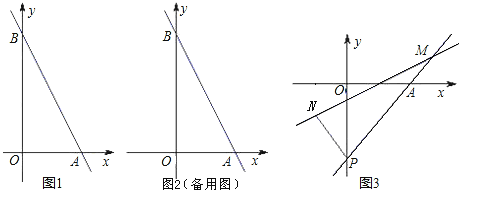
【题目】如图1,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(2,0), B(0,4).
(1)求直线AB的解析式;
(2)若点M为直线y=mx在第一象限上一点,且△ABM是等腰直角三角形,求m的值.
(3)如图3,过点A(2,0)的直线![]() 交y轴负半轴于点P,N点的横坐标为-1,过N点的直线
交y轴负半轴于点P,N点的横坐标为-1,过N点的直线![]() 交AP于点M.求
交AP于点M.求![]() 的值.
的值.
【答案】(1)y=﹣2x+4;(2)m的值是![]() 或
或![]() 或1;(3)2.
或1;(3)2.
【解析】
(1)设直线AB的解析式是y=kx+b,代入得到方程组,求出即可;
(2)当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,证△BMN≌△ABO(AAS),求出M的坐标即可;②当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,同法求出M的坐标;③当AM⊥BM,且AM=BM时,过M作MN⊥x轴于N,MH⊥y轴于H,证△BHM≌△AMN,求出M的坐标即可.
(3)设NM与x轴的交点为H,分别过M、H作x轴的垂线垂足为G,HD交MP于D点,求出H、G的坐标,证△AMG≌△ADH,△AMG≌△ADH≌△DPC≌△NPC,推出PN=PD=AD=AM代入即可求出答案.
(1) ∵A(2,0),B(0,4),
设直线AB的解析式是y=kx+b,
代入得:![]() ,
,
解得:k=﹣2,b=4,
∴直线AB的解析式是y=﹣2x+4.
(2)如图,分三种情况:
①如图①,当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,
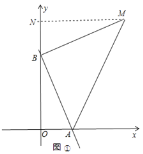
∵BM⊥BA,MN⊥y轴,OB⊥OA,
∴∠MBA=∠MNB=∠BOA=90°,
∴∠NBM+∠NMB=90°,∠ABO+∠NBM=90°,
∴∠ABO=∠NMB,
在△BMN和△ABO中
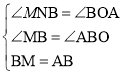 ,
,
∴△BMN≌△ABO(AAS),
MN=OB=4,BN=OA=2,
∴ON=2+4=6,
∴M的坐标为(4,6 ),
代入y=mx得:m=![]() ,
,
②如图②,当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,
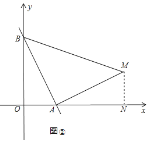
易知△BOA≌△ANM(AAS),
同理求出M的坐标为(6,2),
代入y=mx得:m=![]() ,
,
③如图③,
当AM⊥BM,且AM=BM时,过M作MN⊥X轴于N,MH⊥Y轴于H,

∴四边形ONMH为矩形,
易知△BHM≌△AMN,
∴MN=MH,
设M(x1,x1)代入y=mx得:x1=m x1,
∴
答:m的值是![]() 或
或![]() 或1.
或1.
(3)如图3,设NM与x轴的交点为H,过M作MG⊥x轴于G,过H作HD⊥x轴,
HD交MP于D点,
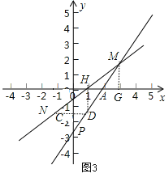
即:∠MGA=∠DHA=900,连接ND,ND 交y轴于C点
由![]() 与x轴交于H点,∴H(1,0),
与x轴交于H点,∴H(1,0),
由![]() 与y=kx﹣2k交于M点,∴M(3,k),
与y=kx﹣2k交于M点,∴M(3,k),
而A(2,0),
∴A为HG的中点,AG=AH,∠MAG=∠DAH
∴△AMG≌△ADH(ASA),∴AM=AD
又因为N点的横坐标为﹣1,且在![]() 上,
上,
∴N(-1,﹣k),同理D(1,﹣k)
∴N关于y轴对称点为D
∴PC是ND的垂直平分线∴PN=PD, CD=NC=HA=1,∠DCP=∠DHA=900,ND平行于X轴
∴∠CDP=∠HAD
∴△ADH≌△DPC ∴AD= PD
∴PN=PD=AD=AM,
∴![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道,4x+2x-x=(4+2-1)x=5x,类似地,我们把(a+b)看成一个整体,则4(a+b)+2(a+b)-(a+b)-(4+2-1)(a+b)=5(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把(a-b)看成一个整体,合并3(a-b)2-7(a-b)2+2(a-b)2的结果是____________.
(2)已知x2-2y=5,求21-![]() x2+y的值;
x2+y的值;
(3)拓广探索:已知a-2b=3,2b-c=-5,c-d=10,求2(a-c)+2(2b-d)-2(2b-c)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
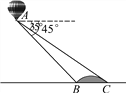
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数:
0,3,8,15,24,…①
2,5,10,17,26,…②
0,6,16,30,48,…③
(1)第①行数按什么规律排的,请写出来?
(2)第②、③行数与第①行数分别对比有什么关系?
(3)取每行的第![]() 个数,求这三个数的和.
个数,求这三个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加射箭比赛,两人各射了5箭,他们的成绩(单位:环)统计如下表.
第1箭 | 第2箭 | 第3箭 | 第4箭 | 第5箭 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 6 | 5 | 7 |
(1)分别计算甲、乙两人射箭比赛的平均成绩;
(2)你认为哪个人的射箭成绩比较稳定?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
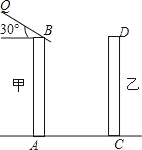
【题目】如图,是住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m,![]() =1.73);
=1.73);
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买20套足球服和一批足球(足球不少于20个),已知A、B两家超市相同型号的产品价格相同,足球服每套240元,足球每个80元。A超市的优惠政策为:每买一套足球服赠送一个足球;B超市的优惠政策为:所有商品一律八折。
(1)设学校计划购买x(x>20)个足球,用含有x的代数式分别表示在A、B两家超市购买所需费用。
(2)若![]() =30,通过计算说明此时按哪种方案购买较为合算?
=30,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
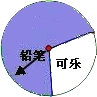
【题目】某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品。下表是活动进行中的一组统计数据:
(1)计算并完成表格:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔”的频率m/n | 0.68 | 0.74 | △ | 0.69 | 0.705 | △ |
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?(精确到1°)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com