
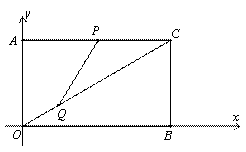
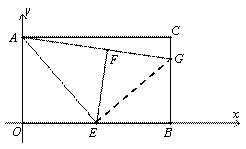
如图,在平面直角坐标系中,矩形AOBC的边长为AO=6,AC=8;
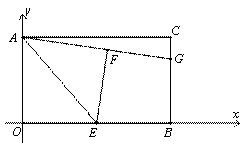
(1)如图①,E是OB的中点,将△AOE沿AE折叠后得到△AFE,点F在矩形AOBC内部,延长AF交BC于点G.求点G的坐标;
(2)定义:若以不在同一直线上的三点中的一点为圆心的圆恰好过另外两个点,这样的圆叫做黄金圆.如图②,动点P以每秒2个单位的速度由点C向点A沿线段CA运动,同时点Q以每秒4个单位的速度由点O向点C沿线段OC运动;求:当 PQC三点恰好构成黄金圆时点P的坐标.
| |||
| |||
|
|
(1) 连接EG,由题意得:DAOE≌DAFE,\?EFG=?OBC=900,
又∵E是OB的中点,\EG=EG,EF=EB=4.
 DEFG≌DEBG.
DEFG≌DEBG.
?FEG=?BEG,?AOB=?AEG=900,
DAOE∽DAEG,AE2=AO×AG,
即36+16=6×AG,AG= ,易得CG=
,易得CG=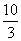 ,BG=
,BG=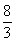 .
.
G的坐标为(8,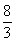 ) .
) .
(2) 设运动的时间为t秒,
当点C为好圆的圆心时,则CQ=CP,
即:2t=10—4t,得到t=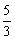 ,此时CP=
,此时CP=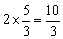 ,AP=
,AP=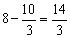 ,
,
P点坐标为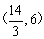 . 当点P为好圆的圆心时,则PC=PQ,
. 当点P为好圆的圆心时,则PC=PQ,
过点Q作AC的垂线交AC于点E,CQ=10—4t,CP=2t.
由三角形相似可知:EQ=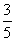 CQ=
CQ= ,
,
PE=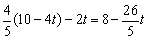 ,
,
则 ,化简得:
,化简得: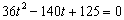 ,
,
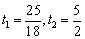 (舍去) .
(舍去) .
此时,AP=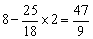 ,P点坐标为
,P点坐标为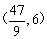 . 当点Q为好圆的圆心时,则QC=PQ,过点Q作AC的垂线交AC于点F,CQ=10—4t,CP=2t,由三角形相似可知:
. 当点Q为好圆的圆心时,则QC=PQ,过点Q作AC的垂线交AC于点F,CQ=10—4t,CP=2t,由三角形相似可知:
QF= ,
,
PF=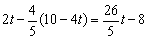 .
.
则 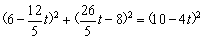 ,整理得
,整理得 .
.
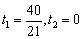 (舍去) .
(舍去) .
此时,AP=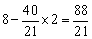 ,P点坐标为
,P点坐标为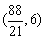 .
.
综上所述,P点坐标为
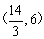 ,
,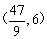 ,
,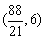 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
某中学开展“中国梦、我的梦”演讲比赛,甲、乙两班 根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
(1)根据下图,分别求出两班复赛的平 均成绩和方差;
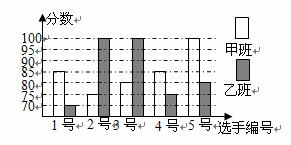
(2)根据(1)的计算结果,分析哪个班级的复赛成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
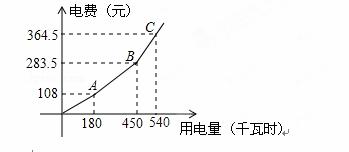
为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如右折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是 元;
(2)第二档的用电量范围是 ;
(3)“基本电价”是 元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com