Question

如图①是一副三角板，其中∠B=∠E=90°，∠A=∠C=45°，∠F=30°，AC=EF=2．把两个三角板ABC和DEF叠放在一起（如图②），且使三角板DEF的直角顶点E与三角板ABC的斜边中点O重合，DE和OC重合．现将三角板DEF绕O点顺时针旋转（旋转角α满足条件：0°＜α＜90°），四边形BGEH是旋转过程中两三角板的重叠部分（如图③）．
（1）当旋转角度为45°时，EG和AB之间的数量关系为______．
（2）当DF经过三角板ABC的顶点B，求旋转角α的度数．
（3）在三角板DEF绕O点旋转的过程中，在DF上是否存在一点P，使得∠APC=90°，若存在，请利用直尺和圆规在DF上画出这个点，并说明理由，若不存在，请说明理由．
（4）在射线EF上取一点M，过M作DF的平行线交射线ED于点N（如图④），若直线MN上始终存在两个点P、Q，使得∠APC=∠AQC=90°，求EM的取值范围．

Answer 1

解：（1）AB=2EG．


（2）过点E作EP⊥DF，垂足是P，

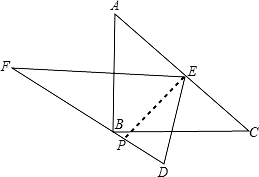
∵∠B=90°，∠A=∠C=45°，AC=2
∴EB=1
∵∠FED=90°，∠F=30°，EF=2
∴EP=1
∴当DF经过三角板ABC的顶点B时，点P与点B重合，
此时∠PED=30°，∠CED=60°
即旋转角α为60°；

（3）以E为圆心，EC为半径画圆，与DF相切于点P，P点即为所求的点．
°
∵∠FED=90°，∠F=30°，EF=2
∴EP=1
∴P点在⊙E上，
∵AC是⊙E直径，
∴∠APC=90°；

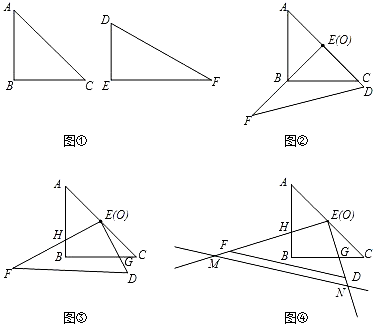
（4）以E为圆心，EC为半径画圆．
当EM＜2时，直线MN和⊙E交于P、Q两点，∠APC=∠AQC=90°．
分析：（1）旋转角度为45°时，EG是△ABC的中位线，根据三角形的中位线定理即可得出EG和AB 之间的数量关系．
（2）当DF经过三角板ABC的顶点B，求旋转角α的度数，即求∠ECD的度数，通过作辅助线可以得到P点与B点重合，从而得到答案．
（3）实际上是圆的切线的性质及判定的运用．
（4）题意告诉我们存在的点要在AC为直径的圆上，所以MN就应该是圆的弦从而得到EM应小于AC的一半．
点评：本题考查了旋转的相关知识，等腰直角三角形的性质、三角形的中位线、圆的切线的性质，圆的割线的运用等知识，难度较大，综合性较强．